Проблема Бернсайда

Проблема Бёрнсайда сформулированная Бёрнсайдом в 1902 году — одна из самых известных и сложных проблем теории групп. Смысл её таков: обязательно ли конечно порождённая группа, в которой каждый элемент имеет конечный порядок, должна быть конечной. Проще говоря, можно ли определить, что группа конечна, исходя лишь из свойств её отдельных элементов.

История

Первоначальные усилия были направлены в сторону положительного решения проблемы, так как все известные частные случаи давали позитивный ответ. Например, если группа порождена 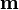$\mathbf{m}$ элементами и порядок каждого её элемента является делителем числа 4, она конечна. Более того, в 1959 году Кострикин (в случае простой экспоненты)^[1] и Зельманов (в общем случае) доказали, что среди конечных групп с данным количеством генераторов и экспонент, существует наибольшая.

Тем не менее, общий ответ на проблему Бернсайда оказался отрицательным. В 1964 году Голод и Шафаревич построили бесконечную группу типа Бернсайда, не предполагая, что каждый элемент имеет равномерно ограниченный порядок. В 1968 году Новиков и Адян предложили отрицательное решение проблемы с ограниченной экспонентой для всех нечетных экспонент больше 4381. В 1982 году Ольшанский нашёл несколько контрпримеров для достаточно больших нечётных экспонент (более 10¹⁰) и предоставил более понятное доказательство, основанное на геометрических идеях.

Случай чётной экспоненты оказался более сложным. В 1992 году С. В. Иванов анонсировал отрицательное решение для достаточно больших чётных экспонент, делящихся на большие степени числа 2 (детальное доказательство было опубликовано в 1994 году и заняло около 300 страниц). Позже в совместной работе Ольшанский и Иванов дали отрицательное решение для аналога проблемы Бёрнсайда для случая гиперболических групп, при условии достаточно большой экспоненты.

Литература

• Кострикин А. И. Вокруг Бёрнсайда. — М.: Наука, 1986 г. — 232 с.
• Ольшанский А. Ю. Геометрия определяющих соотношений в группах. — М.: Наука, 1989. — 446 с.

Примечания

1. ↑ Кострикин А. И. Известия АН СССР // Серия математическая, 1959, т. 23, № 1, с. 3—34.