- Код Рида-Соломона
-
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида — Соломона, работающие с байтами (октетами).
Код Рида — Соломона является частным случаем БЧХ-кода.
В настоящее время широко используется в системах восстановления данных с компакт-дисков, при создании архивов с информацией для восстановления в случае повреждений, в помехоустойчивом кодировании.
Содержание
История
Код Рида — Соломона был изобретён в 1960 году сотрудниками лаборатории Линкольна Массачуссетского технологического института Ирвином Ридом (англ.) и Густавом Соломоном (англ.). Идея использования этого кода была представлена в статье «Polynomial Codes over Certain Finite Fields». Первое применение код Рида — Соломона получил в 1982 году в серийном выпуске компакт-дисков. Эффективный алгоритм декодирования был предложен в 1969 году Элвином Берлекэмпом (англ.) и Джэймсом Месси (англ.)
Формальное описание
Коды Рида — Соломона являются важным частным случаем БЧХ-кода, корни порождающего полинома которого лежат в том же поле, над каким и строится код (m = 1). Пусть α — элемент поля
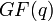 порядка
порядка 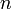 . Если α — примитивный элемент, то его порядок равен q − 1, то есть
. Если α — примитивный элемент, то его порядок равен q − 1, то есть 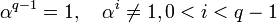 . Тогда нормированный полином g(x) минимальной степени над полем
. Тогда нормированный полином g(x) минимальной степени над полем 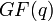 , корнями которого являются d − 1 подряд идущих степеней
, корнями которого являются d − 1 подряд идущих степеней 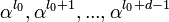 элемента α, является порождающим полиномом кода Рида — Соломона над полем
элемента α, является порождающим полиномом кода Рида — Соломона над полем 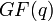 :
: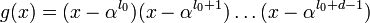
где l0 — некоторое целое число (в том числе 0 и 1), с помощью которого иногда удается упростить кодер. Обычно полагается l0 = 1. Степень многочлена
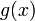 равна d − 1.
равна d − 1.Длина полученного кода n, минимальное расстояние d (минимальное расстояние d линейного кода является минимальным из всех расстояний Хемминга всех пар кодовых слов, см. Линейный код). Код содержит r = d − 1 = deg(g(x)) проверочных символов, где deg() обозначает степень полинома; число информационных символов k = n − r = n − d + 1. Таким образом
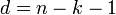 и код Рида — Соломона является разделимым кодом с максимальным расстоянием (является оптимальным в смысле границы Синглтона).
и код Рида — Соломона является разделимым кодом с максимальным расстоянием (является оптимальным в смысле границы Синглтона).Кодовый полином c(x) может быть получен из информационного полинома m(x),
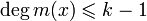 , путем перемножения m(x) и g(x):
, путем перемножения m(x) и g(x):c(x) = m(x)g(x)
Свойства
Код Рида — Соломона над
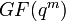 , исправляющий t ошибок, требует 2t проверочных символов и с его помощью исправляются произвольные пакеты длиной t и меньше. Согласно теореме о границе Рейгера, коды Рида — Соломона являются оптимальными с точки зрения соотношения длины пакета и возможности исправления ошибок — используя 2t дополнительных проверочных символов исправляются t ошибок (и менее).
, исправляющий t ошибок, требует 2t проверочных символов и с его помощью исправляются произвольные пакеты длиной t и меньше. Согласно теореме о границе Рейгера, коды Рида — Соломона являются оптимальными с точки зрения соотношения длины пакета и возможности исправления ошибок — используя 2t дополнительных проверочных символов исправляются t ошибок (и менее).Теорема (граница Рейгера). Каждый линейный блоковый код, исправляющий все пакеты длиной t и менее, должен содержать по меньшей мере 2t проверочных символов.
Исправление многократных ошибок
Код Рида — Соломона является одним из наиболее мощных кодов, исправляющих многократные пакеты ошибок. Применяется в каналах, где пакеты ошибок могут образовываться столь часто, что их уже нельзя исправлять с помощью кодов, исправляющих одиночные ошибки.
(qm − 1,qm − 1 − 2t)-код Рида — Соломона над полем
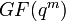 с кодовым расстоянием d = 2t + 1 можно рассматривать как ((qm − 1)m,(qm − 1 − 2t)m)-код над полем
с кодовым расстоянием d = 2t + 1 можно рассматривать как ((qm − 1)m,(qm − 1 − 2t)m)-код над полем 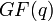 , который может исправлять любую комбинацию ошибок, сосредоточенную в t или меньшем числе блоков из m символов. Наибольшее число блоков длины m, которые может затронуть пакет длины li, где
, который может исправлять любую комбинацию ошибок, сосредоточенную в t или меньшем числе блоков из m символов. Наибольшее число блоков длины m, которые может затронуть пакет длины li, где 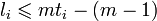 , не превосходит ti, поэтому код, который может исправить t блоков ошибок, всегда может исправить и любую комбинацию из p пакетов общей длины l, если
, не превосходит ti, поэтому код, который может исправить t блоков ошибок, всегда может исправить и любую комбинацию из p пакетов общей длины l, если 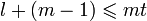 .
.Практическая реализация
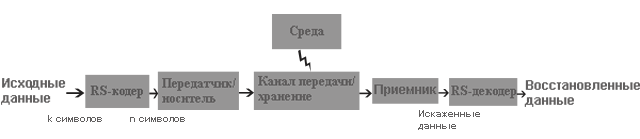
Кодирование с помощью кода Рида — Соломона может быть реализовано двумя способами: систематическим и несистематическим (см. [1], описание кодировщика).
При несистематическом кодировании информационное слово умножается на некий неприводимый полином в поле Галуа. Полученное закодированное слово полностью отличается от исходного и для извлечения информационного слова нужно выполнить операцию декодирования и уже потом можно проверить данные на содержание ошибок. Такое кодирование требует большие затраты ресурсов только на извлечение информационных данных, при этом они могут быть без ошибок.
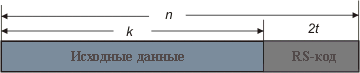 Структура систематического кодового слова Рида — Соломона
Структура систематического кодового слова Рида — СоломонаПри систематическом кодировании к информационному блоку из k символов приписываются 2t проверочных символов, при вычислении каждого проверочного символа используются все k символов исходного блока. В этом случае нет затрат ресурсов при извлечении исходного блока, если информационное слово не содержит ошибок, но кодировщик/декодировщик должен выполнить k(n − k) операций сложения и умножения для генерации проверочных символов. Кроме того, так как все операции проводятся в поле Галуа, то сами операции кодирования/декодирования требуют много ресурсов и времени. Быстрый алгоритм декодирования, основанный на быстром преобразовании Фурье, выполняется за время порядка lnn2.
Кодирование
При операции кодирования информационный полином умножается на порождающий многочлен. Умножение исходного слова S длины k на неприводимый полином при систематическом кодировании можно выполнить следующим образом:
- К исходному слову приписываются 2t нулей, получается полином
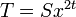 .
. - Этот полином делится на порождающий полином G, находится остаток R,
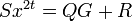 , где Q — частное.
, где Q — частное. - Этот остаток и будет корректирующем кодом Рида — Соломона, он приписывается к исходному блоку символов. Полученное кодовое слово
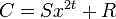 .
.
Кодировщик строится из сдвиговых регистров, сумматоров и умножителей. Сдвиговый регистр состоит из ячеек памяти, в каждой из которых находится один элемент поля Галуа.
Декодирование
Декодировщик, работающий по авторегрессивному спектральному методу декодирования, последовательно выполняет следующие действия:
- Вычисляет синдром ошибки
- Строит полином ошибки
- Находит корни данного полинома
- Определяет характер ошибки
- Исправляет ошибки
Вычисление синдрома ошибки
Вычисление синдрома ошибки выполняется синдромным декодером, который делит кодовое слово на порождающий многочлен. Если при делении возникает остаток, то в слове есть ошибка. Остаток от деления является синдромом ошибки.
Построение полинома ошибки
Вычисленный синдром ошибки не указывает на положение ошибок. Степень полинома синдрома равна 2t, что много меньше степени кодового слова n. Для получения соответсвия между ошибкой и ее положением в сообщении строится полином ошибок. Полином ошибок реализуется с помощью алгоритма Берлекэмпа — Месси, либо с помощью алгоритма Евклида. Алгоритм Евклида имеет простую реализацию, но требует больших затрат ресурсов. Поэтому чаще применяется более сложный, но менее затратоемкий алгоритм Берлекэмпа — Месси. Коэффициенты найденного полинома непосредственно соответствуют коэффициентам ошибочных символов в кодовом слове.
Нахождение корней
На этом этапе ищутся корни полинома ошибки, определяющие положение искаженных символов в кодовом слове. Реализуется с помощью процедуры Ченя, равносильной полному перебору. В полином ошибок последовательно подставляются все возможные значения, когда полином обращается в ноль — корни найдены.
Определение характера ошибки и ее исправление
По синдрому ошибки и найденным корням полинома с помощью алгоритма Форни определяется характер ошибки и строится маска искаженных символов. Эта маска накладывается на кодовое слово с помощью операции XOR и искаженные символы восстанавливаются. После этого отбрасываются проверочные символы и получается восстановленное информационное слово.
Применение
В настоящий момент коды Рида — Соломона имеют очень широкую область применения благодаря их способности находить и исправлять многократные пакеты ошибок.
Запись и хранение информации
Код Рида — Соломона используется при записи и чтении в контроллерах оперативной памяти, при архивировании данных, записи информации на жесткие диски (
Запись на CD-ROM
Возможные ошибки при чтении с диска появляются уже на этапе производства диска, так как сделать идеальный диск при современных технологиях невозможно. Так же ошибки могут быть вызваны царапинами на поверхности диска, пылью и т. д. Поэтому при изготовлении читаемого компакт-диска используется система коррекции CIRC (Cross Interleaved Reed Solomon Code). Эта коррекция реализована во всех устройствах, позволяющих считывать данные с CD дисков, в виде чипа с прошивкой firmware. Нахождение и коррекция ошибок основана на избыточности и перемежении (redundancy & interleaving). Избыточность примерно 25 % от исходной информации.
При записи на цифровые аудиокомпакт-диски (Compact Disc Digital Audio — CD-DA) используется стандарт Red Book. Коррекция ошибок происходит на двух уровнях C1 и C2. При кодировании на первом этапе происходит добавление проверочных символов к исходным данным, на втором этапе информация снова кодируется. Кроме кодирования осуществляется также перемешивание (перемежение) байтов, чтобы при коррекции блоки ошибок распались на отдельные биты, которые легче исправляются. На первом уровне обнаруживаются и исправляются ошибочные блоки длиной один и два байта (один и два ошибочных символа соответсвенно). Ошибочные блоки длиной три байта обнаруживаются и передаются на следующий уровень. На втором уровне обнаруживаются и исправляются ошибочные блоки, возникшие в C2, длиной 1 и 2 байта. Обнаружение трех ошибочных символа является фатальной ошибкой, не могут быть исправлены.
Беспроводная и мобильная связь
Этот алгоритм кодирования используется при передаче данных по сетям оптических линиях связи, в спутниковой и радиорелейной связи. Метод прямой коррекции ошибок в проходящем трафике (Forward Error Correction, FEC) основывается на кодах Рида — Соломона.
Примеры кодов
16-ричный (15,11) код Рида — Соломона
Пусть t = 2,l0 = 1. Тогда
g(x) = (x − α)(x − α2)(x − α3)(x − α4) = x4 + α13x3 + α6x2 + α3x + α10
.
Степень g(x) равна 4, n − k = 4 и k = 11. Каждому элементу поля GF(16) можно сопоставить 4 бита. Информационный многочлен является последовательностью 11 символов из GF(16), что эквивалентно 44 битам, а все кодовое слово является набором из 60 бит.
8-ричный (7,3) код Рида — Соломона
Пусть t = 2,l0 = 4. Тогда
g(x) = (x − α4)(x − α5)(x − α6)(x − α0) = x4 + α6x3 + α6x2 + α3x + α
.
Пусть информационный многочлен имеет вид
m(x) = α4x2 + x + α3
.
Кодовое слово несистематического кода запишется в виде
c(x) = m(x)g(x) = (α4x2 + x + α3)(x4 + α6x3 + α6x2 + α3x + α) = α4x6 + αx5 + α6x4 + 0x3 + 0x2 + α5x + α4
что представляет собой последовательность семи восьмеричных символов.
Примечания
Литература
- Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976. — С. 596.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and practice of error control codes. — М.: Мир, 1986. — С. 576.
- Берлекэмп Э. Алгебраическая теория кодирования = Algebraic Coding Theory. — М.: Мир, 1971. — С. 478.
Ссылки
- Могущество кодов Рида — Соломона или информация, воскресшая из пепла (статья Криса Касперски)
- Помехоустойчивое кодирование в пакетных сетях (статья В. Варгаузина)
- Error Correcting Code (ECC)
- CD-R диски, технология изнутри
- Формат CD
См. также
- К исходному слову приписываются 2t нулей, получается полином
Wikimedia Foundation. 2010.
