- 0,(9)
-
0,(9) или 0,999… (
 ) («ноль и девять в периоде») — периодическая десятичная дробь, представляющая число 1. Другими словами,
) («ноль и девять в периоде») — периодическая десятичная дробь, представляющая число 1. Другими словами,У этого равенства существует несколько доказательств, основанных на теории пределов.
Содержание
Доказательства
Алгебраические
Деление столбиком
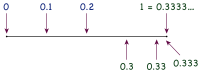
Часто рациональная дробь может быть представлена десятичной только с бесконечным хвостом. Используя деление столбиком, деление двух целых чисел, например 1⁄3 приводит к бесконечному 0,333… в десятичной записи, где цифры повторяются бесконечно. Таким образом легко доказывается равенство 0,999… = 1. Умножение 3 на 3 даёт 9 в каждом разряде, поэтому 3 × 0,333… эквивалентно 0,999…. И 3 × 1⁄3 эквивалентно 1, поэтому 0,999… = 1[1].


Манипуляции с цифрами
Когда число в десятичной записи умножается на 10, то цифры не меняются, но каждый разряд передвигается на одну цифру влево. Следовательно, 10 × 0,999… = 9,999…, что на 9 больше, чем исходное число. Чтобы это увидеть, отнимем 0,999… от 9,999…, каждая цифра после запятой исчезает, так как 9 — 9 = 0 для каждого разряда. Последний шаг использует правила алгебры:
Аналитические
Число 0,999… в общем виде можно записать как

Бесконечные последовательности
В соответствии с определением позиционной системы счисления, посчитаем сумму ряда:
Для 0,999… применим теорему о сумме сходящейся геометрической прогрессии[2]:
- Если
 , то
, то 
Радиус сходимости (знаменатель прогрессии)
 , и таким образом:
, и таким образом:Такое доказательство (об эквивалентности 10 и 9,999…) было опубликовано в 1770 году Леонардом Эйлером в издании Элементы алгебры (англ.)[3].
Формула суммы сходящейся геометрической прогрессии была известна до Эйлера. Выпущенный в 1811 году учебник An Introduction to Algebra также использует геометрическую прогрессию для числа 0,(9)[4]. В XIX веке реакция на такое правило суммирования вылилась в утверждение: сумма ряда должна быть пределом последовательности частичных сумм[5].
Последовательность (x0, x1, x2, …) имеет предел x тогда и только тогда, когда |x − xn| бесконечна мала с ростом n. Утверждение 0.999… = 1 может быть интерпретировано как предел[6]:
Последний шаг
 — делается на основании того, что вещественные числа удовлетворяют аксиоме Архимеда.
— делается на основании того, что вещественные числа удовлетворяют аксиоме Архимеда.Применение
Существует много применений, например в элементарной теории чисел. В 1802 году H. Goodwin опубликовал наблюдение, обнаруженное им при делении на простые числа. Например:
- 1/7 = 0,142857142857… и 142 + 857 = 999.
- 1/73 = 0,0136986301369863… и 0136 + 9863 = 9999.
Миди в 1836 году обобщил данные наблюдения до теоремы Миди (англ.).
В популярной культуре
Новостная колонка The Straight Dope доказывает 0,999… с помощью 1⁄3 и пределов, говоря о непонимании,
Низший примат в нас упирается, говоря: ,999~ на самом деле представляет не число, а процесс. Чтобы найти число мы должны остановить этот процесс. И в этот момент равенство ,999~ = 1 просто разваливается. Чушь.[7]
Вопрос о 0,999… стал такой популярной темой в первые семь лет форумов Battle.net, что компания выпустила «пресс-релиз» на День дураков 2004 года:
Мы очень рады закрыть книгу на этой теме раз и на всегда. Мы были свидетелями страдания и беспокойства насчёт того, ,999~ равняется 1 или же нет, и мы с гордостью представляем следующее доказательство, решаюшее эту проблему для наших покупателей[8].
Далее следуют доказательства, основанные на пределах и умножении на 10.
См. также

0,(9) на Викискладе? Примечания
- ↑ cf. with the binary version of the same argument in Silvanus P. Thompson, Calculus made easy, St. Martin’s Press, New York, 1998. ISBN 0-312-18548-0.
- ↑ Rudin p.61, Theorem 3.26; J. Stewart p.706
- ↑ Euler p.170
- ↑ Grattan-Guinness p.69; Bonnycastle p.177
- ↑ For example, J. Stewart p.706, Rudin p.61, Protter and Morrey p.213, Pugh p.180, J.B. Conway p.31
- ↑ The limit follows, for example, from Rudin p. 57, Theorem 3.20e. For a more direct approach, see also Finney, Weir, Giordano (2001) Thomas' Calculus: Early Transcendentals 10ed, Addison-Wesley, New York. Section 8.1, example 2(a), example 6(b).
- ↑ Cecil Adams An infinite question: Why doesn't .999~ = 1?. The Straight Dope. Chicago Reader (11 июля 2003). Архивировано из первоисточника 18 февраля 2012. Проверено 6 сентября 2006.
- ↑ Blizzard Entertainment Announces .999~ (Repeating) = 1. Press Release. Blizzard Entertainment (1 апреля 2004). Архивировано из первоисточника 18 февраля 2012. Проверено 16 ноября 2009.
 Категория:
Категория:- Числа
Wikimedia Foundation. 2010.