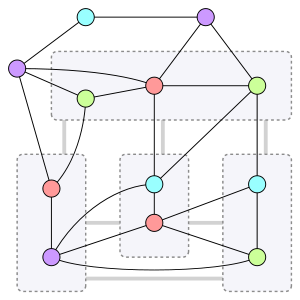
- Гипотеза Хадвигера
-
Не следует путать с проблемой Нелсона — Эрдеша — Хадвигера.
Гипотеза Хадвигера — одна из неразрешённых гипотез теории графов. Она формулируется следующим образом: всякий k-хроматический граф стягиваем к полному графу на
 вершинах.
вершинах.Содержание
Другие формулировки
Гипотезу Хадвигера можно сформулировать иначе: в каждом
 -хроматическом графе обязательно существует
-хроматическом графе обязательно существует  непересекающихся связных подграфов таких, что между любыми двумя из них есть ребро.
непересекающихся связных подграфов таких, что между любыми двумя из них есть ребро.Если ввести для графа число Хадвигера
 — максимальное
— максимальное  такое, что
такое, что  стягиваем к полному графу на
стягиваем к полному графу на  вершинах, то гипотеза формулируется в виде неравенства
вершинах, то гипотеза формулируется в виде неравенства  , где
, где  — хроматическое число графа.
— хроматическое число графа.Частные случаи
Случаи
 и
и  очевидны: в первом случае граф содержит хотя бы одно ребро, которое и является полным графом
очевидны: в первом случае граф содержит хотя бы одно ребро, которое и является полным графом  , во втором случае граф не является двудольным и содержит цикл, стягиваемый к
, во втором случае граф не является двудольным и содержит цикл, стягиваемый к  .
.Доказательство в случае
 было опубликовано самим Хадвигером в той же работе, в которой была поставлена гипотеза.
было опубликовано самим Хадвигером в той же работе, в которой была поставлена гипотеза.Из гипотезы Хадвигера в случае
 следует справедливость проблемы четырёх красок (ныне доказаной): операция стягивания сохраняет планарность, и, если бы существовал планарный 5-хроматический граф, то существовало бы вложение графа
следует справедливость проблемы четырёх красок (ныне доказаной): операция стягивания сохраняет планарность, и, если бы существовал планарный 5-хроматический граф, то существовало бы вложение графа  в плоскость, несуществование которого следует из формулы Эйлера. В 1937 году Клаус Вагнер доказал равносильность проблемы четырёх красок и гипотезы Хадвигера при
в плоскость, несуществование которого следует из формулы Эйлера. В 1937 году Клаус Вагнер доказал равносильность проблемы четырёх красок и гипотезы Хадвигера при  , таким образом, этот случай также доказан.
, таким образом, этот случай также доказан.В 1993 году Н. Робертсон, П. Сеймур и Р. Томас доказали гипотезу для
 , используя проблему четырёх красок.[1] Это доказательство получило премию Фалкерсона в 1994 году.
, используя проблему четырёх красок.[1] Это доказательство получило премию Фалкерсона в 1994 году.Для
 известно, что если граф не удовлетворяет гипотезе, то он стягиваем и к
известно, что если граф не удовлетворяет гипотезе, то он стягиваем и к  , и к
, и к  — полным двудольным графам на 4 и 4 и 3 и 5 вершинах соответственно.
— полным двудольным графам на 4 и 4 и 3 и 5 вершинах соответственно.Число Хадвигера
Можно определить отображение
 , сопоставляющее графу
, сопоставляющее графу  максимальное
максимальное  такое, что
такое, что  стягиваем к полному графу на
стягиваем к полному графу на  вершинах. Вычисление числа Хадвигера данного графа — NP-полная задача. В любом графе
вершинах. Вычисление числа Хадвигера данного графа — NP-полная задача. В любом графе  таком, что
таком, что  существует вершина степени не более
существует вершина степени не более  .[2] Применяя жадный алгоритм для раскраски графа, из этого утверждения можно вывести, что
.[2] Применяя жадный алгоритм для раскраски графа, из этого утверждения можно вывести, что  .
.
Примечания
- ↑ Robertson, Neil; Seymour, Paul; Thomas, Robin (1993), «Hadwiger’s conjecture for K6-free graphs»
- ↑ Kostochka, A. V. (1984), "Lower bound of the Hadwiger number of graphs by their average degree"
Категории:- Теория графов
- Математические гипотезы
Wikimedia Foundation. 2010.