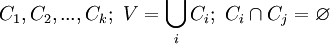Раскраска графа

3-раскраска графа Петерсена

Хроматическое число графа G — минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета. Обозначается χ(G).

Определение

Хроматическое число графа — минимально количество непересекающихся классов вершин графа

$C_1, C_2, ..., C_k;\ V=\bigcup_i^{} C_i;\ C_i\cap C_j=\varnothing$

(где V — множество вершин графа), таких, что вершины в каждом классе независимы, то есть что любое ребро графа не соединяет вершины одного и того же класса.

Связанные определения

• Граф называется K-раскрашиваемым, если его хроматическое число не превосходит K, а K не превосходит количества вершин графа. То есть
  • граф называется K-раскрашиваемым, если его вершины можно раскрасить K разными цветами так, что у любого ребра концы будут разного цвета.
• K-хроматический граф — граф, хроматическое число которого равно K. То есть
  • граф называется K-хроматическим, если его вершины можно покрасить минимум K цветами так, что у любого ребра концы будут разного цвета. K при этом называется хроматическим числом этого графа.

Реберная раскраска

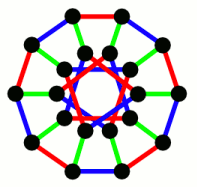реберная раскраска кубического графа

Хроматический класс графа G — минимальное число цветов, в которые можно раскрасить ребра графа G так, чтобы смежные ребра имели разные цвета. Обозначается χ'(G). Проблема реберной раскраски произвольного плоского кубического графа без мостов тремя цветами эквивалентна знаменитой Проблеме четырех красок. Реберная раскраска определяет 1-факторизацию графа.

Хроматический многочлен

Если рассмотреть количество различных раскрасок помеченного графа как функцию от доступного числа цветов t, то оказывается, что эта функция всегда будет полиномом от t. Этот факт был обнаружен Биркгофом и Льюисом ^[1] при попытке доказать Гипотезу четырех красок.

Хроматические многочлены некоторых графов

Треугольник K3	t(t − 1)(t − 2)
Полный граф Kn	t(t − 1)(t − 2)...(t − (n − 1))
Дерево с n вершинами	t(t − 1)n − 1
Цикл Cn	(t − 1)n + ( − 1)n(t − 1)
Граф Петерсена	t(t − 1)(t − 2)(t7 − 12t6 + 67t5 − 230t4 + 529t3 − 814t2 + 775t − 352)

Значение для теории графов

Множество глубоких задач теории графов легко формулируются в терминах раскраски. Самая знаменитая из таких задач, Проблема четырёх красок, в настоящее время решена, однако появляются новые, например, обобщение Проблемы четырёх красок, гипотеза Хадвигера.

Литература

«Теория графов» — О. Оре, перевод с английского И. Н. Врублевской, под редакцией Н. Н. Воробьева, издательство «Наука», Москва 1986

1. ↑ Birkhoff, G. D. and Lewis, D. C. "Chromatic Polynomials." Trans. Amer. Math. Soc. 60, 355-451, 1946.