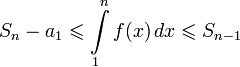- Интегральный признак Коши — Маклорена
-
Интегральный признак Коши — Маклорена
Интегральный признак Коши-Маклорена — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на
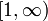 , последний часто может быть найден в явном виде.
, последний часто может быть найден в явном виде.Содержание
Формулировка теоремы
Пусть для функции f(x) выполняется:
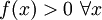 (функция принимает только положительные значения)
(функция принимает только положительные значения)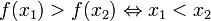 (функция монотонно убывает)
(функция монотонно убывает)- f(n) = an
Тогда ряд
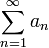 и несобственный интеграл
и несобственный интеграл 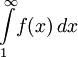 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.Набросок доказательства
- Построим на графике f(x) ступенчатые фигуры как показано на рисунке
- Площадь большей фигуры равна Sb = f(1) + f(2) + f(3) + ... + f(n − 1)
- Площадь меньшей фигуры равна Ss = f(2) + f(3) + f(4) + ... + f(n)
- Площадь криволинейной трапеции под графиком функции равна
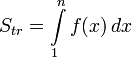
- Получаем
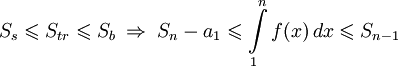
- Далее доказывается с помощью критерия сходимости знакоположительных рядов.
Примеры
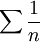 расходится так как
расходится так как 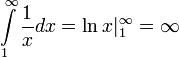 .
.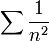 сходится так как
сходится так как 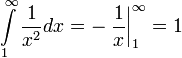 .
.
Оценка остатка ряда
Интегральный признак Коши позволяет оценить остаток rn знакоположительного ряда. Из полученного в доказательстве выражения
с помощью несложных преобразований получаем:
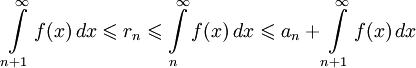 .
.
См. также
Wikimedia Foundation. 2010.
Интегральный признак Коши — У этого термина существуют и другие значения, см. Признак Коши. Интегральный признак Коши Маклорена признак сходимости убывающего положительного числового ряда. Признак Коши Маклорена даёт возможность свести проверку сходимости ряда к… … Википедия
Признак Коши — Термин «признак Коши» может относиться к одному из следующих утверждений: Радикальный признак Коши Интегральный признак Коши Маклорена Критерий Коши См. также Теорема Коши … Википедия
Признак сходимости д’Аламбера — Признак д’Аламбера признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г. Если для числового ряда существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство … Википедия
КОШИ ПРИЗНАК — 1) К. п. сходимости числового ряда: если для числового ряда с неотрицательными членами существует такое число что, начиная с нек рого номера, выполняется неравенство равносильное условию то данный ряд сходится. Если же, начиная с нек рого номера … Математическая энциклопедия
Признак Ермакова — признак сходимости числовых рядов с положительными членами, установленный Василием Ермаковым. Его специфика заключается в том, что он превосходит все прочие признаки своей чувствительностью . Эта работа опубликована в статьях: «Общая теория… … Википедия
Признак Жамэ — признак сходимости числовых рядов с положительными членами, установленный Пьером Жамэ. Содержание 1 Формулировка 2 Формулировка в предельной форме … Википедия
Абсолютная сходимость — У этого термина существуют и другие значения, см. Сходимость. Сходящийся ряд называется сходящимся абсолютно, если сходится ряд из модулей , иначе сходящимся условно. Аналогично, если несобственный интеграл от функции сходится, то он… … Википедия
Ряд — I бесконечная сумма, например вида u1 + u2 + u3 +... + un +... или, короче, Одним из простейших примеров Р., встречающихся уже в элементарной математике, является сумма бесконечно убывающей… … Большая советская энциклопедия
Ряд (математич.) — Ряд, бесконечная сумма, например вида u1 + u2 + u3 +... + un +... или, короче, . (1) Одним из простейших примеров Р., встречающихся уже в элементарной математике, является сумма бесконечно убывающей геометрической прогрессии 1 + q + q 2 +... + q… … Большая советская энциклопедия
РЯД — б е с к о н е ч н а я с у м м а, последовательность элементов (наз. ч л е н а м и д а н н о г о р я д а) нек рого линейного топологич. пространства и определенное бесконечное множество их конечных сумм (наз. ч а с т и ч н ы м и с у м м а м и р я… … Математическая энциклопедия