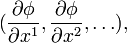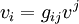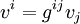1-форма

1-форма

1-фо́рма (пфа́ффова фо́рма) — дифференциальная форма степени 1, ковариантное тензорное поле валентности 1 на касательном расслоении многообразия. Понятие синонимично полю ковариантного вектора. Чаще всего встречающемся примером 1-формы в математике является дифференциал.

Особые случаи

Пусть 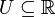$U \subseteq \mathbb{R}$ - область. Рассмотрим функцию 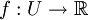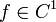$f: U \to \mathbb{R}$, $f\in C^1$. Дифференциал df функции f, в точке 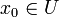$x_0\in U$, определён как линейное отображение переменных dx. Имеем 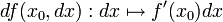$df(x_0, dx): dx \mapsto f'(x_0) dx$. (Значение символа dx таково: он есть просто аргументом, независимой переменной, функции df.) Поэтому отображение 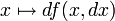$x \mapsto df(x,dx)$ отображает каждый x в линейный функционал df(x,dx).

1-форма называется замкнутой, если она дифференцируемая, а её внешняя производная везде равна нулю.

Введение

Говоря проще, ковариантный вектор — это такой объект, который действует на обычный контравариантный вектор и в результате даёт число — скалярное произведение этих векторов с обычными свойствами линейности. Размерность ковекторов совпадает с размерностью их контравариантных аналогов.

• Это определение согласовано с определением ковариантного тензора валентности 1 (см. Тензор), каковым и является ковариантный вектор (ковектор) в качестве частного случая тензора.

Нередко ковариантным вектором, особенно в физической литературе, называют разложение любого вектора (то есть вектора или ковектора, вектора касательного или кокасательного пространства) по дуальному базису. Тогда речь идёт о наборе ковариантных координат любого объекта — 1-формы или обычного вектора, обычно, однако, каждый тип объектов стараются записывать в естественном для него базисе, что соответствует основному определению.

Ковариантные координаты любого объекта принято записывать с нижним индексом, а также — в матричных обозначениях — в виде вектора-строки (в отличие от записи с верхним индексом и вектора-столбца для контравариантных координат, естественных для представления контравариантного вектора).

• Возможно, было бы лучше строго придерживаться различия в понимании терминов «ковектор» и «ковариантный вектор», понимая под первым объект (вектор ко-касательного пространства — 1-форму), а под вторым — представление с нижним индексом любого объекта, однако с одной стороны — изоморфизм между ко- и просто касательным пространствами в случае (псевдо-)римановых многообразий всё равно размывает формальную границу в этом самом распространённом случае, а с другой стороны — традиция применения термина к тензорам достаточно устойчива. Кроме того, подъём-опускание индекса возможны всё-таки не во всех случаях, а при этом свойства представления будут жёстко закреплены за самим объектом.

Простое «традиционное» определение ковариантного вектора из учебника Ландау^[1]:

«Ковариантным вектором называется всякая совокупность [равного размерности пространства количества] величин, которые при преобразовании координат преобразуются как производные от скаляра».

Под производными от скаляра имеются тут в виду производные от скалярной функции по (контравариантным) координатам:

$(\frac{\partial \phi}{\partial x^1},\frac{\partial \phi}{\partial x^2},\dots),$

а вектор, согласно «традиционному» подходу определяется как набор его координат, изменяющихся определённым образом при замене базиса (системы координат).

Как видим, формально это определение описывает ковариантное представление, но содержательно описывает в качестве образца ковариантного вектора ковектор — 1-форму — градиент скаляра — для которой (как и для остальных 1-форм) именно это представление естественно^[2].

Ко- и контравариантные векторы в пространствах (на многообразиях) с невырожденной метрикой

Далее подразумевается, что на пространстве, в котором существуют описанные объекты (или на многообразии, в касательном пространстве которого они существуют) задана невырожденная метрика.

Соответствие между векторами и ковекторами

Если определён невырожденный метрический тензор, то формально «ковариантный вектор» и «контравариантный вектор» можно считать просто разными представлениями (записями в виде набора чисел) одного и того же геометрического объекта — обычного вектора. То есть один и тот же вектор может быть записан как ковариантный (то есть через набор ковариантных координат) или контравариантный (то есть через набор контравариантных координат). Преобразование одного представления в другое осуществляется просто свёрткой с метрическим тензором:

$\ v_i = g_{ij} v^j$

$\ v^i = g^{ij} v_j$

(здесь и ниже подразумевается суммирование по повторяющемуся индексу, по правилу Эйнштейна).

Различие между векторами и ковекторами

Содержательно векторы и ковекторы различают по тому, какое из представлений для них естественно. Так, для ковекторов, например, для градиента — естественно разложение по дуальному базису, так как их естественная свертка (скалярное произведение) с обычным вектором (например, смещением) осуществляется без участия метрики, просто суммированием перемноженных компонент. Для обычных же векторов (к которым принадлежит и само смещение по пространственным координатам dxⁱ) — естественно разложение по главному базису, так как они свёртываются с другими обычными векторами, такими, как вектор смещения по пространственным координатам, с участием метрики. Например, скаляр 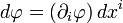$\ d\varphi = (\partial_i \varphi)\,dx^i$ получается (как полный дифференциал) свёртыванием без участия метрики ковариантного вектора 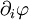$\ \partial_i \varphi$, являющегося естественным представлением 1-формы градиента, подействовавшей на скалярное поле, с контравариантным вектором 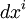$\ dx^i$, являющимся естественным представлением обычного вектора смещения по координатам; при этом сам с собой 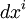$\ dx^i$ свёртывается с помощью метрики: 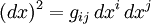$\ (dx)^2 = g_{ij}\, dx^i\, dx^j$, что находится в полном согласии с тем, что он контравариантный.

Если речь идёт об обычном физическом пространстве, простым признаком ковариантности — контравариантрности вектора является то, как свёртывается его естественное представление с набором координат пространственного перемещения 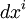$\ dx^i$, являющегося образцом контравариантного вектора. Те, что свертываются с 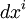$\ dx^i$ посредством простого суммирования, без участия метрики, — это ковариантные векторы (1-формы), в противном случае (свёртка требует участия метрики) — это контравариантные векторы. Если же пространство и координаты полностью абстрактны и нет способа различить главный и дуальный базис, кроме как произвольным условным выбором, то содержательное различие между ковариантными и контравариантными векторами пропадает или становится также чисто условным.

Вопрос о том, является ли именно то представление, в каком мы видим объект, естественным для него, затронут уже чуть выше. Естественным для обычного вектора является контравариантное представление, для ковектора же — ковариантное.

Примечания

1. ↑ * Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7, стр. 298
2. ↑ Естественность ковариантного предствыления 1-формы градиента означает, что ее естественное представление — набор частных производных 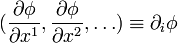$(\frac{\partial \phi}{\partial x^1},\frac{\partial \phi}{\partial x^2},\dots) \equiv \partial_i \phi$ — дает в скалярном произведении с контравариантным вектором dxⁱ инвариант 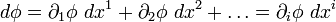$d\phi = \partial_1 \phi \ dx^1 + \partial_2 \phi\ dx^2 + \dots = \partial_i \phi\ dx^i$ — полный дифференциал функции ф, конечно же, инвариантный (в последней формуле подразумевается суммирование по индексу i по правилу Эйнштейна).

См. также

• Изоморфизм между касательным и кокасательным пространством
• Ковариантность и контравариантность
• Контравариантный вектор

Литература

Математическая энциклопедия. — М.: Советская энциклопедия, 1979. — Т. 2. — 552 с. — 150 000 экз.