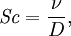- Шмидта число
-
Число Шмидта (обозн. Sc) — безразмерное число, показывающее соотношение интенсивностей диффузии импульса (то есть вязкость) и диффузии вещества. Оно является критерием подобия для течений жидкости, в которых наблюдаются одновременно как переносы вещества (обычно примеси), так и вязкие эффекты.
По одной версии число было названо в честь немецкого инженера Эрнста Шмидта, по другой — в честь австрийского геофизика Вильгельма Матеуса Шмидта.
Число Шмидта равно отношению коэффициентов кинематической вязкости к коэффициенту диффузии вещества (или коэффициенту массопереноса). Оно также равно отношению толщин гидродинамического пограничного слоя и слоя массопереноса.
Определение числа Шмидта [1] в виде формулы:
где:
- ν — кинематическая вязкость [ м²·с-1],
- D — коэффициент диффузии [ м²·с-1].
Таким образом, его величина показывает, насколько импульс переносится эффективнее вещества.
В совершенных газах Sc = 1, так как ν = D; в реальных газах оно может отличаться от 1 на десятки процентов. В жидкостях оно порядка 1000, в жидких металлах порядка 10.
Аналог числа Шмидта для переноса тепла — число Прандтля. В связи с этим, число Шмидта часто называют диффузионным числом Прандтля и обозначают PrD.
См. также
Безразмерные числа в физике Понятия Размерность физической величины · Безразмерное число · П-теорема · Критерий подобия Числа Аббе · Архимеда · Багнольда · Био · Бонда · Бринкмана · Вебера · Вайсенберга · Гагена · Галилея · Гартмана · Грасхофа · Гуше · Дамкёлера · Деборы · Дерягина · Гретца · Дина · Каулинга · капиллярности · Кнудсена · Лапласа · Льюиса · Маха · Марангони · Нуссельта · Онезорге · Пекле · Прандтля (магнитное, турбулентное) · Рейнольдса (магнитное) · Ричардсона · Россби · Роуза · Рошко · Руарка · Рэлея · Стентона · Стокса · Струхаля · Суратмана · Тейлора · Уомерсли · Фруда · Фурье · Чандрасекара · Шмидта · Шервуда · Эйлера · Эккерта · Экмана · Элсассера · Эотвоша Примечания
- ↑ Frank P. Incropera, David P. DeWitt «Основы тепло- и массопереноса» = „Fundamentals of Heat and Mass Transfer“ // 3rd Ed.. — 1990. — С. p. 345. — ISBN 0-471-51729-1. Eq. 6.71.
Wikimedia Foundation. 2010.