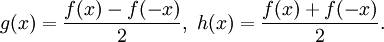Чётные и нечётные функции

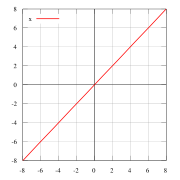f(x) = x — пример нечётной функции.

f(x) = x² — пример чётной функции.

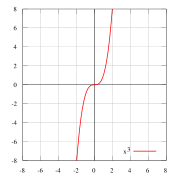f(x) = x³, нечётная

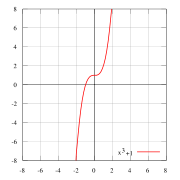f(x) = x³ + 1 ни чётная, ни нечётная

Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Или по-другому

Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Определения

• Функция $f:[-X,X] \subset \mathbb{R} \to \mathbb{R}$ называется нечётной, если справедливо равенство

$f(-x)=-f(x), \quad \forall x \in [-X,X].$

• Функция f называется чётной, если справедливо равенство

$f(-x) = f(x),\quad \forall x \in [-X,X].$

• Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.

Свойства

• График нечётной функции симметричен относительно начала координат O.
• График чётной функции симметричен относительно оси ординат Oy.
• Произвольная функция $f:[-X,X] \subset \mathbb{R} \to \mathbb{R}$ может быть представлена в виде суммы нечётной и чётной функций:

f(x) = g(x) + h(x),

где

$g(x) = \frac{f(x) - f(-x)}{2},\; h(x) = \frac{f(x)+f(-x)}{2}.$

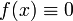• Функция $f(x) \equiv 0$ — единственная функция, одновременно являющаяся нечётной и чётной.
• Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
• Произведение или дробь двух нечётных функций чётно.
• Произведение или дробь двух чётных функций чётно.
• Произведение или дробь нечётной и чётной функций нечётно.
• Композиция двух нечётных функция нечётна.
• Композиция двух чётных функций чётна.
• Композиция чётной функции с нечётной чётна.
• Композиция любой функции с чётной чётна (но не наоборот).
• Функция, обратная чётной, чётна, а нечётной — нечётна.
• Производная чётной функции нечётна, а нечётной — чётна.
  • То же верно про производную третьего, пятого и вообще любого нечётного порядка.
• Производная чётного порядка сохраняет чётность.

Примеры

Нечётные функции

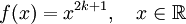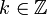• Нечётная степень $f(x) = x^{2k+1},\quad x\in \mathbb{R}$ где $k\in \mathbb{Z}$ — произвольное целое число.
• Синус $f(x) = \sin x,\quad x \in \mathbb{R}$.
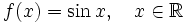• Тангенс $f(x) = \operatorname{tg} x,\quad x \in \mathbb{R}$.

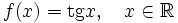Чётные функции

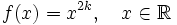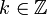• Чётная степень $f(x) = x^{2k},\quad x\in \mathbb{R}$ где $k\in \mathbb{Z}$ — произвольное целое число.
• Косинус $f(x) = \cos x,\quad x \in \mathbb{R}$.

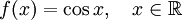Вариации и обобщения

• Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.