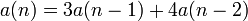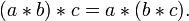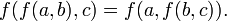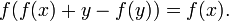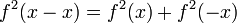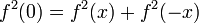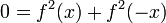- Функциональные уравнения
-
В математике функциональным уравнением называется уравнение, выражающее связь между значением функции (или функций) в одной точке с ее значениями в других точках. Свойства функций, например, могут быть определены с учетом типов функциональных уравнений, за что они отвечают. Термин функциональное уравнение как правило используется для уравнений которые не в простом смысле, сводятся к алгебраическим уравнениям, часто потому, что две или более известных функций заменяются в качестве аргумента в другую функцию. Часто встречаются на различных математических соревнованиях.
Содержание
Примеры
- Решение функционального уравнения
- удовлетворяет Дзета-функция Римана ζ где Γ(z) — Гамма-функция Эйлера.
- Решением этих уравнений является Гамма-функция. Гамма-функция является единственным решением этой системы всех трех уравнений:
- Функциональное уравнене
- где a, b, c, d являются целыми числами удовлетворяющими равенство ad − bc = 1, т.е.
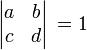 , откуда следует что
, откуда следует что  является унитарной матрицей (т.е. имеющей определитель 1), определяет f как модулярную форму порядка k.
является унитарной матрицей (т.е. имеющей определитель 1), определяет f как модулярную форму порядка k.
- Различные примеры, не обязательно связанные с "знаменитыми" функциями:
-
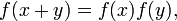 удовлетворяют все показательные функции
удовлетворяют все показательные функции
-
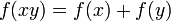 , удовлетворяют все логарифмические функции
, удовлетворяют все логарифмические функции
-
![f(x + y) + f(x - y) = 2[f(x) + f(y)]\,\!](/pictures/wiki/files/101/e40ac4d8f084d1e56a6e8ca6a56fc13f.png) (квадратное уравнение или закон паралелограмма)
(квадратное уравнение или закон паралелограмма)
-
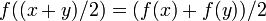 (Йенсен)
(Йенсен)
-
![g(x + y) + g(x - y) = 2[g(x) g(y)]\,\!](/pictures/wiki/files/101/eb5d1c90c36d56cc8d6abbf49d9ffc5c.png) (д'Аламбер)
(д'Аламбер)
-
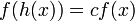 (Уравнение Шредера)
(Уравнение Шредера)
-
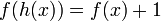 (Уравнение Абеля).
(Уравнение Абеля).
- Простой формой функионального уравнения является реккурентное соотношение. Это, формально говоря, связано с неизвестной функцией от целых чисел, а также перевода операторов.
- Одним из примеров реккурентного соотношения является
- Коммутативный и ассоциативный законы функциональных уравнений. Когда ассоциативный закон выражается в виде его знакомой формы, что позволяет некоторым символом между двумя переменными представляет собой бинарную операцию:
Но если мы напишем f(a,b) вместо a * b, то ассоциативный закон будет выглядеть как то, что обычно называют функциональным уравнением:
One thing that all of the examples listed above share in common is that in each case two or more known functions (sometimes multiplication by a constant, sometimes addition of two variables, sometimes the identity function) are substituted into the unknown function to be solved for.
- The b-integer and b-decimal parts of real numbers were introduced and studied by M.H.Hooshmand [1]. The b-parts real functions have many interesting number theoretic explanations, analytic and algebraic properties, and satisfy the functional equation:
The following functional equations are as a generalization of the b-parts functional equation for semigroups and groups, even in a binary system (magma), that are introduced by him:
Associative equations ;
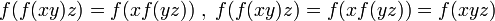
Decomposer equations ;
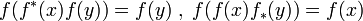
Strong decomposer equations ;
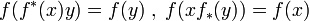
Canceler equations ;
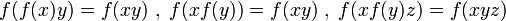
where f * (x)f(x) = f(x)f * (x) = x. In [2], the general solution of the decomposer and strong decomposer equations are introduced in the sets with a binary operation and semigroups respectively and also associative equations in arbitrary groups. In that paper it is proven that the associative equations and the system of strong decomposer and canceler equations do not have any nontrivial solutions in the simple groups.
When it comes to asking for all solutions, it may be the case that conditions from mathematical analysis should be applied; for example, in the case of the Cauchy equation mentioned above, the solutions that are continuous functions are the 'reasonable' ones, while other solutions that are not likely to have practical application can be constructed (by using a Hamel basis for the real numbers as vector space over the rational numbers). The Bohr-Mollerup theorem is another well-known example.Решение функциональных уравнений
Решение функциональных уравнений может быть очень трудным, но существуют некоторые общие методы их решения.
Обсуждение инволюции функции полезно. Например, рассмотрим функцию
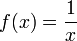 .
.
Затем рассмотрим
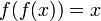 ,
,
если мы продолжим схему мы в конце получим x при четном количестве композиций и f(x) при нечетном. Эта же идея распространяется на многие другие функции, например,
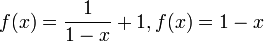 и многие другие.
и многие другие.
Пример 1: Решить
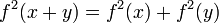 для всех
для всех 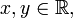 где f принимает вещественные значения.
где f принимает вещественные значения.Положим x = y = 0: f2(0) = f2(0) + f2(0). Тогда f2(0) = 0 и f(0) = 0.
Теперь, положим y = − x:
Квадрат вещественного числа неотрицателен, и сумма неотрицательных чисел равна нулю тогда и только тогда когда оба числа равны 0. Значит f2(x) = 0 для всех x и
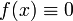 является единственным решением этого уравнения.
является единственным решением этого уравнения.
Пример 2: Найти все функции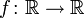 , такие что для любых
, такие что для любых 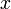 и
и 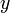 выполняется условие:
выполняется условие: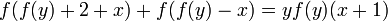
Положим x = − 1. Тогда
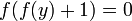
Если предположить, что
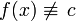 , то
, то 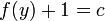 откуда следует что все равно
откуда следует что все равно 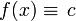 .
.Значит
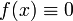 .
.См. также
Внешние ссылки
- Functional Equations: Exact Solutions at EqWorld: The World of Mathematical Equations.
- Functional Equations: Index at EqWorld: The World of Mathematical Equations.
- IMO Compendium text on functional equations in problem solving.
Ссылки
- Marek Kuczma : Functional equations in a single variable (Polska Akademia Nauk. Monografie matematyczne, t. 46)
- M. Kuczma, On the functional equation φn(x) = g(x). Ann. Polon. Math. 11 (1961) 161-175
- ↑ M.H.Hooshmand, (2005). "b-Digital sequences". Wmsci 2005: 9Th World Multi-Conference on Systemics, Cybernetics and Informatics 8: 142–146.
- ↑ M.H.Hooshmand, H.K.Haili (2007). "Decomposer and associative functional equations". Indagationes Mathematicae 18 (4): 539–554. DOI:10.1016/S0019-3577(07)80061-9.
Wikimedia Foundation. 2010.

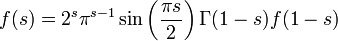
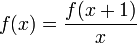
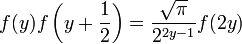
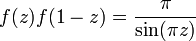 (
(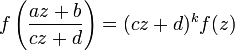
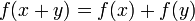 (
(