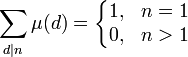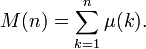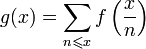Формулы обращения Мёбиуса
- Формулы обращения Мёбиуса
-
Функция Мёбиуса μ(n) — мультипликативная арифметическая функция, применяемая в теории чисел и комбинаторике, названа в честь немецкого математика Мёбиуса, который впервые рассмотрел её в 1831 г.
Определение
μ(n) определена для всех натуральных чисел n и принимает значения 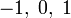 в зависимости от характера разложения числа n на простые сомножители:
в зависимости от характера разложения числа n на простые сомножители:
- μ(n) = 1 если n свободно от квадратов (т.е. не делится на квадрат никакого простого числа) и разложение n на простые множители состоит из чётного числа сомножителей;
- μ(n) = − 1 если n свободно от квадратов и разложение n на простые множители состоит из нечётного числа сомножителей;
- μ(n) = 0 если n не свободно от квадратов.
По определению также полагают μ(1) = 1.
Свойства и приложения
Функция Мёбиуса мультипликативна: для любых взаимно простых чисел a и b выполняется равенство μ(ab) = μ(a)μ(b).
Сумма значений функции Мёбиуса по всем делителям целого числа n, не равного единице, равна нулю
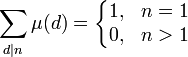
Отсюда, в частности, следует, что для всякого непустого конечного множества количество различных подмножеств состоящих из нечётного числа элементов равно количеству различных подмножеств состоящих из чётного числа элементов — факт, применяемый в доказательстве формулы обращения Мёбиуса.
Функция Мёбиуса связана с функцией Мертенса отношением
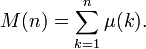
Функция Мертенса в свою очередь тесно связана с задачей о нулях дзета-функции Римана, см. статью гипотеза Мертенса.
Обращение Мёбиуса
Первая формула обращения Мёбиуса
Для арифметических функций f и g,
-
тогда и только тогда, когда
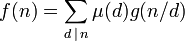 .
.
Вторая формула обращения Мёбиуса
Для вещественнозначных функций f(x) и g(x), определеных при 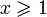 ,
,
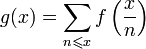
тогда и только тогда, когда
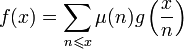 .
.
Здесь сумма 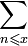 интерпретируется как
интерпретируется как 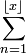 .
.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Формулы обращения Мёбиуса" в других словарях:
Формулы обращения Мебиуса — Функция Мёбиуса μ(n) мультипликативная арифметическая функция, применяемая в теории чисел и комбинаторике, названа в честь немецкого математика Мёбиуса, который впервые рассмотрел её в 1831 г. Содержание 1 Определение 2 Свойства и приложения … Википедия
Формула обращения Мебиуса — Функция Мёбиуса μ(n) мультипликативная арифметическая функция, применяемая в теории чисел и комбинаторике, названа в честь немецкого математика Мёбиуса, который впервые рассмотрел её в 1831 г. Содержание 1 Определение 2 Свойства и приложения … Википедия
Функция Мёбиуса — мультипликативная арифметическая функция, применяемая в теории чисел и комбинаторике, названа в честь немецкого математика Мёбиуса, который впервые рассмотрел её в 1831 году. Содержание 1 Определение … Википедия
Обращение Мёбиуса — Функция Мёбиуса μ(n) мультипликативная арифметическая функция, применяемая в теории чисел и комбинаторике, названа в честь немецкого математика Мёбиуса, который впервые рассмотрел её в 1831 г. Содержание 1 Определение 2 Свойства и приложения … Википедия
МЁБИУСА РЯД — функциональный ряд вида М. р. исследовап А. Мёбиусом [1], к рый нашел для ряда (*) формулу обращения: где Мёбиуса функция. А. Мёбиус рассмотрел также формулы обращения для конечных сумм по делителям заданного натурального числа п: Другая формула… … Математическая энциклопедия
Формула включений-исключений — (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия
Обращение Мебиуса — Функция Мёбиуса μ(n) мультипликативная арифметическая функция, применяемая в теории чисел и комбинаторике, названа в честь немецкого математика Мёбиуса, который впервые рассмотрел её в 1831 г. Содержание 1 Определение 2 Свойства и приложения … Википедия
Функция Мебиуса — Функция Мёбиуса μ(n) мультипликативная арифметическая функция, применяемая в теории чисел и комбинаторике, названа в честь немецкого математика Мёбиуса, который впервые рассмотрел её в 1831 г. Содержание 1 Определение 2 Свойства и приложения … Википедия
Теорема о распределении простых чисел — Теорема о распределении простых чисел теорема аналитической теории чисел, описывающая асимптотику распределения простых чисел. А именно, она утверждает, что функция распределения простых чисел (количество простых чисел на отрезке от 1 до n) … Википедия
Функция распределения простых чисел — В математике функция распределения простых чисел или пи функция это функция равная числу простых чисел, меньше либо равных действительному числу x.[1][2] Она обозначается (это никак не связано с числом пи) … Википедия
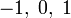 в зависимости от характера разложения числа n на простые сомножители:
в зависимости от характера разложения числа n на простые сомножители: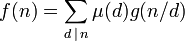 .
.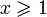 ,
,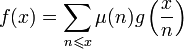 .
.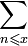 интерпретируется как
интерпретируется как 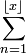 .
.