Резольвентнoe множество

Спектр оператора — множество чисел, характеризующее линейный оператор. Применяется в линейной алгебре, функциональном анализе и квантовой механике.

Конечномерный случай

Пусть A — оператор, действующий в конечномерном линейном пространстве E. Спектром оператора называется множество всех его собственных значений.

Квадратную матрицу n×n можно рассматривать как линейный оператор в n-мерном пространстве, что позволяет перенести на матрицы «операторные» термины. В таком случае говорят о спектре матрицы.

Общее определение

Пусть A — оператор, действующий в банаховом пространстве E над полем k. Число λ называется регулярным для оператора A, если оператор R(λ) = (A − λI) ^{− 1}, называемый резольвентой оператора A, определён на всём E и непрерывен. Множество регулярных значений оператора A называется резольвентным множеством этого оператора, а дополнение резольвентного множества — спектром этого оператора. Спектр оператора представляет собой непустой^[1] компакт в k. Обычно в качестве k рассматривают комплексную плоскость $\mathbb C$.

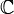Внутри спектра оператора можно выделять части, не одинаковые по своим свойствам. Одной из основных классификаций спектра является следующая:

1. дискретным (точечным) спектром называется множество всех собственных значений оператора A — только точечный спектр присутствует в конечномерном случае;
2. непрерывным спектром называется множество значений λ, при которых резольвента (A - λI) ^{- 1} определена на всюду плотном множестве в E, но не является непрерывной;
3. остаточным спектром называется множество точек спектра, не входящих ни в дискретную, ни в непрерывную части.

Максимум модулей точек спектра оператора A называется спектральным радиусом этого оператора и обозначается через r(A). При этом выполняется равенство $r(A) = \lim_{n \to \infty} \|A^n\|^{1/n}$.

В комплексном случае резольвента является голоморфной операторнозначной функцией на резольвентном множестве. В частности, при λ > r(A) она может быть разложена в ряд Лорана с центром в точке z = 0.

примечания

1. ↑ При условиях:
   • Во-первых, поле k является алгебраически замкнутым (например, поле комплексных чисел);
   • Во-вторых, пространство E имеет размерность больше нуля.

В квантовой механике

Спектр самосопряжённых операторов играет важную роль в квантовой механике, определяя множество возможных значений наблюдаемой при измерении. В частности, спектр гамильтониана определяет допустимые уровни энергии квантовой системы.

См. также

• Проектор (алгебра)
• Спектр алгебры

Ссылки