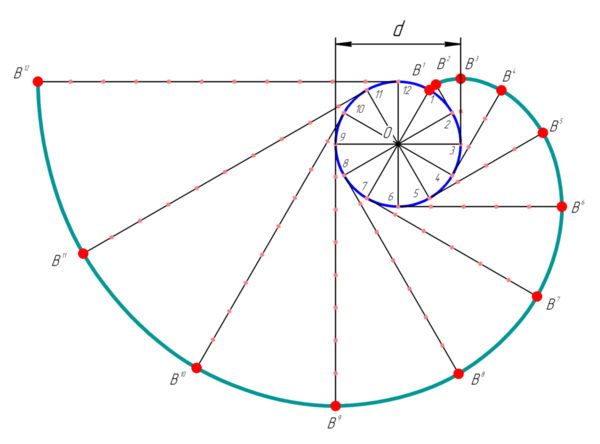
Развертка окружности

Эвольвентой окружности является траектория любой точки прямой линии, перекатываемой по окружности без скольжения. По эвольвенте обрабатывают профиль зубьев зубчатых колёс. Эвольвенту окружности можно получить, сматывая натянутую нить с цилиндрической поверхности. Конец этой нити будет описывать эвольвенту.

Параметрические уравнения эвольвенты окружности:

$x=r \cos\phi+r\phi \sin\phi\,\!;$
$y=r \sin\phi-r\phi \cos\phi\,\!,$

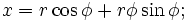
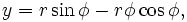
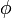где $r\,\!$— радиус окружности; $\phi\,\!$— угол поворота радиуса окружности.

Построение эвольвенты окружности по заданному диаметру

Имеется окружность с диаметром 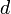$d\!$, и с центром в точке 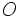$O\!$. Данную окружность делим на двенадцать равных частей. В точках 2, 3, 4, … проводим касательные к окружности, направленные в одну сторону. Точки эвольвенты находим исходя из того, что при развёртывании окружности точка 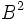$B^2\!$, должна отстоять от точки 2 на расстоянии, равном длине дуги между точками 1 и 2, а точка 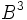$B^3\!$, должна отстоять от точки 3 на расстоянии, равном длине дуги между точками 1 и 3 (две длины предыдущей дуги), и т. д.

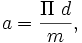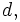Точное положение точек эвольвенты получим, откладывая по касательным длины соответствующих дуг. Длину дуги между точками 1 и 2 определяем по формуле $a=\frac {\Pi\ d}{m},\!$, где $d,\!$ — диаметр окружности; 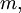$m,\!$ — число частей, на которое разделена окружность.

Получив ряд точек эвольвенты соединяем их плавной линией.

В данном случае окружность с диаметром 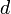$d\!$ является эволютой к этой эвольвенте.

Эвольвента окружности

См. также

• Эвольвента
• Эвольвентное зацепление
• Зубчатая передача

Литература

1. Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению.. — М.: Машиностроение., 1989. — С. 438-480. — 864 с. — ISBN 5-217-00403-7