- Эвольвентное зацепление
-
Эвольвентное зацепление позволяет передавать движение с постоянным передаточным отношением[1] [2]. Эвольвентное зацепление — зубчатое зацепление, в котором профили зубьев очерчены по эвольвенте окружности.
Для этого необходимо чтобы зубья зубчатых колёс были очерчены по кривой, у которой общая нормаль, проведённая через точку касания профилей зубьев, всегда проходит через одну и ту же точку на линии, соединяющей центры зубчатых колёс, называемую полюсом зацепления[3].
Содержание
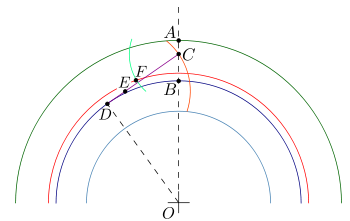
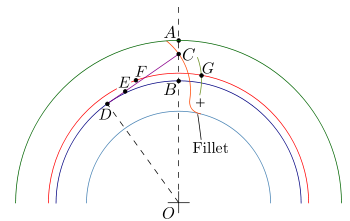
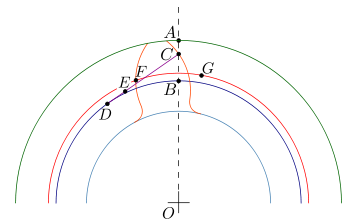
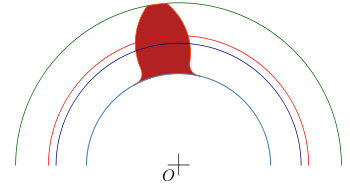
Построение эвольвентного зацепления
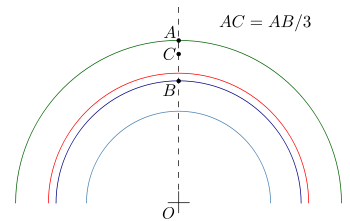
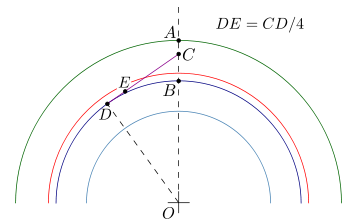
Способ приближённого построения эвольвентного зубчатого зацепления. Подходит для технических рисунков, построенных от руки или с помощью САПР.
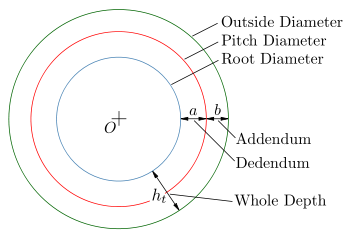
Перед построением необходимо задать следующие размеры:
- высота ножки зуба
 (на рис. обозначена a);
(на рис. обозначена a); - высота головки зуба
 (на рис. обозначена b);
(на рис. обозначена b); - диаметр начальной окружности
 (на рис. обозначен D);
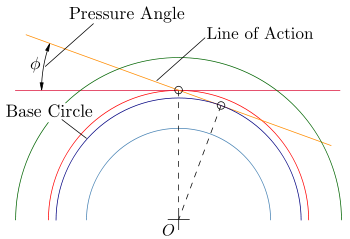
(на рис. обозначен D); - угол зацепления
 (на рис. обозначен φ);
(на рис. обозначен φ); - окружная толщина зуба st;
- радиус кривизны переходной кривой в граничной точке профиля ρf.
Перед построением эвольвентного зацепления необходимо рассчитать его геометрические параметры. Предположим, что даны числа зубьев колеса
 и шестерни
и шестерни  , указан тип зацепления: нулевое, равносмещенное или неравносмещенное. Сначала исходя из типа по таблицам или блокирующему контуру нужно выбрать коэффициенты смещения
, указан тип зацепления: нулевое, равносмещенное или неравносмещенное. Сначала исходя из типа по таблицам или блокирующему контуру нужно выбрать коэффициенты смещения  и
и  .
.Стандартизация
В соответствии с принципом взаимозаменяемости ряд геометрических параметров эвольвентного зацепления стандартизован. В России зубчатые колёса выбирают по числу зубьев
 и модулю
и модулю  , принимая следующие параметры за постоянные (по ГОСТ 13755-81[4]):
, принимая следующие параметры за постоянные (по ГОСТ 13755-81[4]):- высота головок зуба
 ;
; - глубина впадин
 ;
; - подрезания нет, то есть
 или угол зацепления
или угол зацепления  равен основному углу зацепления
равен основному углу зацепления  ;
; - угол зацепления
 °;
°; - коэффициент высоты головки зуба
 ;
; - коэффициент радиального зазора
 .
.
В США и Великобритании вместо модуля используется питч
 , Питч - величина обратная модулю.
, Питч - величина обратная модулю.См. также
- Зацепление Новикова
- Эксцентриково-циклоидальное зацепление
- Эвольвента
- Эвольвента окружности
- Механическая передача
Примечания
- ↑ Теоретически эквивалентно качению без скольжения друг по другу двух окружностей которые называются начальными окружностями.
- ↑ Предложено в 1754 г. Леонардом Эйлером.
- ↑ Стоить отметить, что кроме эвольвентного зацепления, удовлетворяющему этому требованию, существует циклоидальное и круговое (Новикова) зацепление.
- ↑ ГОСТ 13755-81. Основные нормы взаимозаменяемости. Передачи зубчатые цилиндрические эвольвентные. Исходный контур
Категория:- Механические передачи
- высота ножки зуба
Wikimedia Foundation. 2010.