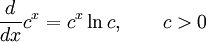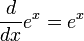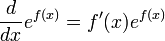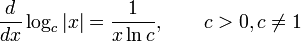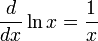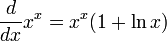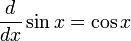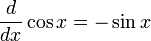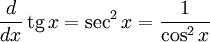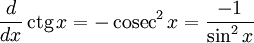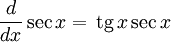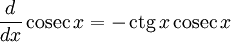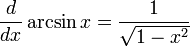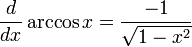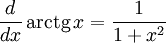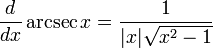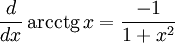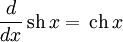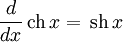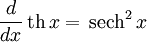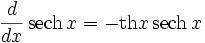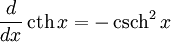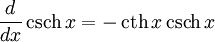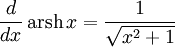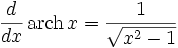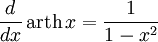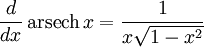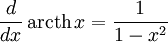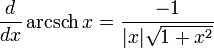Производные основных элементарных функций
Полезное
Смотреть что такое "Производные основных элементарных функций" в других словарях:
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия интеграла, его свойства и методы вычислений. И. и. непрерывно связано с дифференциальным исчислением и составляет вместе с ним основу математич. анализа. Истоки И. и. относятся к античному периоду… … Математическая энциклопедия
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ — функция, обратная к показательной функции. Л. ф. обозначается ее значение у, соответствующее значению аргумента х, наз. натуральным логарифмом числа х. В силу определения соотношение (1) равносильно Так как при любом действительном у, то Л. ф.… … Математическая энциклопедия
Медицина — I Медицина Медицина система научных знаний и практической деятельности, целями которой являются укрепление и сохранение здоровья, продление жизни людей, предупреждение и лечение болезней человека. Для выполнения этих задач М. изучает строение и… … Медицинская энциклопедия
Дифференциальное исчисление — раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную математическую дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 … Большая советская энциклопедия
Тригонометрические функции — один из важнейших классов элементарных функций. Для определения Т. ф. обычно рассматривают окружность единичного радиуса с двумя взаимно перпендикулярными диаметрами A A и B B (рис. 1). От точки А по окружности откладываются дуги … Большая советская энциклопедия
СССР. Естественные науки — Математика Научные исследования в области математики начали проводиться в России с 18 в., когда членами Петербургской АН стали Л. Эйлер, Д. Бернулли и другие западноевропейские учёные. По замыслу Петра I академики иностранцы… … Большая советская энциклопедия
НАУКА — особый вид познавательной деятельности, направленный на выработку объективных, системно организованных и обоснованных знаний о мире. Взаимодействует с др. видами познавательной деятельности: обыденным, художественным, религиозным, мифологическим … Философская энциклопедия
ГРИНА ФУНКЦИЯ — функция, связанная с интегральным представлением решений краевых задач для дифференциальных уравнений. Г. ф. краевой задачи для линейного дифференциального уравнения фундаментальное решение уравнения, удовлетворяющее однородным краевым условиям.… … Математическая энциклопедия
ВЕРОЯТНОСТЕЙ ТЕОРИЯ — занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера
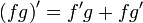 (известно как «правило Лейбница»)
(известно как «правило Лейбница»)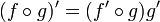 — правило дифференцирования сложной функции
— правило дифференцирования сложной функции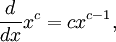 когда
когда 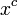 и
и 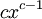 определены
определены
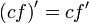
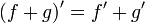
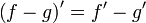
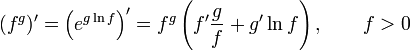
![{d \over dx} \sqrt [n] {x} = {d \over dx} x^{1\over n} = {1 \over n} x^{-{n-1\over n}} = \frac {1} {n \cdot \sqrt [n] {x^{n-1}}}](/pictures/wiki/files/97/a1aad2ace76e34508b0e326eed13e815.png)