Правило трех сигм

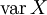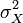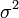Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, т. е. её отклонения от математического ожидания. Обозначается D[X] в русской литературе и $\operatorname{var}\,X$ (англ. variance) в зарубежной. В статистике часто употребляется обозначение $\sigma_X^2$ или $\displaystyle \sigma^2$. Квадратный корень из дисперсии 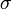$\displaystyle \sigma$ называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом.

Определение

Пусть 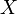$\displaystyle X$ — случайная величина, определённая на некотором вероятностном пространстве. Тогда

$D[X] = M\left[(X -M[X])^2\right],$

где символ M обозначает математическое ожидание.

Замечания

• В силу линейности математического ожидания справедлива формула:

$D[X] = M[X^2] - \left(M[X]\right)^2;$

• Дисперсия является вторым центральным моментом случайной величины;
• Дисперсия может быть бесконечной. См., например, распределение Коши.
• Дисперсия может быть вычислена с помощью производящей функции моментов U(t):

D[X] = U''(0) − U'²(0)

• Дисперсия целочисленной случайной величины может быть вычислена с помощью производящей функции последовательности.

Свойства дисперсии

• Дисперсия любой случайной величины неотрицательна: $D[X] \geqslant 0;$
• Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;
• Если случайная величина равна константе, то её дисперсия равна нулю: D[a] = 0. Верно и обратное: если D[X] = 0, то X = M[X] п.н.
• Пусть 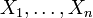$\displaystyle X_1,\dots, X_n$ — случайные величины, а 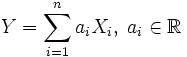$Y = \sum\limits_{i=1}^n a_i X_i,\; a_i\in \mathbb{R}$ — их произвольная линейная комбинация. Тогда

$D[Y] = \sum\limits_{i=1}^n a_i^2 D[X_i] + \sum\limits_{i\not = j} a_i a_j\,\operatorname{cov}\,(X_i,X_j) = \sum\limits_{i=1}^n a_i^2 D[X_i] + 2 \sum\limits_{i < j} a_i a_j\,\operatorname{cov}\,(X_i,X_j),$

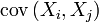где $\operatorname{cov}\,(X_i,X_j)$ — ковариация случайных величин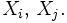 $\displaystyle X_i,\, X_j.$

В частности:

• $D\left[ X_1 + \cdots + X_n\right] = D[X_1] +\dots +D[X_n],$

если $\displaystyle X_1,\ldots , X_n$ независимы;

• $D\left[aX\right] = a^2D[X];$
• $D\left[-X\right] = D[X];$
• $D\left[X+b\right] = D[X].$

Пример

Пусть случайная величина 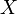$\displaystyle X$ имеет стандартное непрерывное равномерное распределение на $\displaystyle [0,1],$ т. е. её плотность вероятности задана равенством

$f_X(x) = \left\{ \begin{matrix} 1, & x\in [0,1] \\ 0, & x \not\in [0,1]. \end{matrix} \right.$

Тогда

$M\left[X^2\right] = \int\limits_0^1\!x^2\, dx = \left. \frac{x^3}{3}\right\vert_0^1 = \frac{1}{3},$

и

$M\left[X\right] = \int\limits_0^1\! x\, dx = \left. \frac{x^2}{2}\right\vert_0^1 = \frac{1}{2}.$

Тогда

$D[X] = M\left[X^2\right] - (M[X])^2 = \frac{1}{3} - \left(\frac{1}{2}\right)^2 = \frac{1}{12}.$

См. также

• Моменты случайной величины;
• Ковариация;
• Выборочная дисперсия;
• Выборочное стандартное отклонение;
• Независимость (теория вероятностей).
• Скедастичность