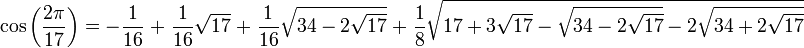Построения с помощью циркуля и линейки

Построения с помощью циркуля и линейки — раздел евклидовой геометрии, известный с античных времён.

В задачах на построение возможны следующие операции:

• Отметить произвольную точку на плоскости, точку на одной из построенных линий или точку пересечения двух построенных линий.
• С помощью циркуля провести окружность с центром в построенной точке с радиусом, равным расстоянию между двух уже построенных точек.
• С помощью линейки провести прямую, проходящую через две построенные точки.

При этом циркуль и линейка считаются идеальными инструментами, в частности

• Линейка не имеет делений и имеет только одну сторону бесконечной длины.
• Циркуль может иметь сколь угодно большой раствор.

Простой пример

Разбиение отрезка пополам

Задача. С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:

• Циркулем проводим окружность с центром в точке A радиусом AB.
• Проводим окружность с центром в точке B радиусом AB.
• Находим точки пересечения P и Q двух построенных окружностей.
• Линейкой проводим отрезок, соединяющий точки P и Q.
• Находим точку пересечения AB и PQ. Это — искомая середина отрезка AB.

Правильные многоугольники

Основная статья: Теорема Гаусса — Ванцеля

Построение правильного пятиугольника

Античным геометрам были известны способы построения правильных n-угольников для 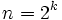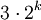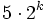$n=2^k\,\!$, $3\cdot 2^k$, $5\cdot 2^k$ и $3\cdot5\cdot2^k$.

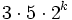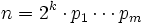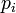Гаусс показал в 1796 возможность построения правильных n-угольников при $n=2^k\cdot p_1\cdots p_m$, где $p_i\,\!$ — различные простые числа Ферма. В 1836 П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.

Известные задачи

• Задача Аполлония
• Задача Брахмагупты

Неразрешимые задачи

Следующие три задачи на построение были поставлены ещё в античности:

• Трисекция угла — разбить произвольный угол на три равные части.
• Удвоение куба — построить отрезок, являющийся ребром куба в два раза большего объёма, чем куб с данным ребром.
• Квадратура круга — построить квадрат, равный по площади данному кругу.

Только в XIX веке было доказано, что все три задачи не имеют решения. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.

Возможные и невозможные построения

Все построения являются ничем иным, как решениями какого-либо уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа. В рамках вышеописанных требований, возможны следующие построения:

• Построение решений линейных уравнений.
• Построение решений квадратных уравнений.

Иначе говоря, возможно построить лишь числа равные арифметическим выражениям с использованием квадратного корня из исходных чисел (длин отрезков). Например,

• Если задан только отрезок длины 1, то $\sqrt[3]{2}$ невозможно представить в таком виде (отсюда невозможность удвоения куба).
• Возможность построить правильный 17-угольник следует из выражения на косинус угла:

  $\cos{\left(\frac{2\pi}{17}\right)} = -\frac{1}{16} \; + \; \frac{1}{16} \sqrt{17} \;+\; \frac{1}{16} \sqrt{34 - 2 \sqrt{17}} \;+\; \frac{1}{8} \sqrt{ 17 + 3 \sqrt{17} - \sqrt{34 - 2 \sqrt{17}} - 2 \sqrt{34 + 2 \sqrt{17}} }$

Вариации и обобщения

• Построения с помощью одного циркуля. По теореме Мора — Маскерони с помощью одного циркуля можно построить любую фигуру, которую можно построить циркулем и линейкой. При этом прямая считается построенной, если на ней заданы две точки.
• Построения с помощью одной линейки. Легко заметить, что с помощью одной линейки можно проводить только проективно-инвариантные построения. В частности, невозможно даже разбить отрезок на две равные части, либо найти центр нарисованной окружности. Но при наличии на плоскости заранее проведённой окружности с отмеченным центром с помощью линейки можно провести те же построения, что и циркулем и линейкой (теорема Понселе — Штейнера (англ.)), 1833.
• Построения с помощью плоского оригами. см. правила Худзита

Забавные факты

• Узор на флаге Ирана описывается как построение с помощью циркуля и линейки, (см. [1] на персидском).

См.также

• Kig,

Литература

• А. Адлер. Теория геометрических построений, Перевод с немецкого Г. М. Фихтенгольца. Издание третье. Л., Учпедгиз, 1940—232 с.
• И. И. Александров, Сборник геометрических задач на построение, Издание восемнадцатое, М., Учпедгиз, 1950—176 с.
• Б. И. Аргунов, М Б Балк. Геометрические построения на плоскости, Пособие для студентов педагогических институтов. Издание второе. М., Учпедгиз, 1957—268 с.
• А. М. Воронец. Геометрия циркуля, Популярная библиотека по математике под общей редакцией Л. А. Люстерника, М.- Л., ОНТИ, 1934 — 40 с.
• В. А. Гейлер. Неразрешимые задачи на построение, СОЖ, 1999, No 12, с. 115—118.
• Ю. И.  Манин, О разрешимости задач на построение с помощью циркуля и линейки, Энциклопедия элементарной математики книга четвёртая (геометрия), М., Физматгиз, 1963. — 568с.
• Ю. Петерсен. Методы и теории решения геометрических задач на построение, Москва, типография Э.Лисснера и Ю.Романа, 1892 — VIII + 114с.
• В. В. Прасолов Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга, М.: Наука, 1992. 80 с. Серия Популярные лекции по математике, выпуск 62
• Я. Штейнер, Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга, М., Учпедгиз, 1939 — 80 с.
• Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 80. — 383 с. — ISBN 5-09-001287-3