Правила Худзита

Правила Худзита

Правила Худзита — набор из семи правил формально описывающие геометрические построения с помощью плоского оригами, подобным построениям с помощью циркуля и линейки.

Фактически они описывают все возможные способы получения одной новой складки на листе бумаги, путем совмещения уже существующих различных элементов листа — точек и линий. Под линиями подразумеваются края листа или складки бумаги, под точками — пересечения линий. Существенным моментом является то, что сгиб формируется единственной складкой, причем в результате складывания фигура остается плоской.

Часто эти правила называют «аксиомами», хотя с формальной точки зрения аксиомами они не являются.

Правила

Складки в этих правилах существуют не всегда, правило утверждает только, что если такая складка есть, то её «можно» найти.

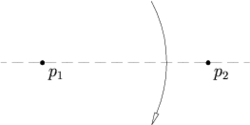
Правило 1

Пусть заданы две точки p₁ и p₂, тогда лист можно сложить так, что данные две точки будут лежать на складке.

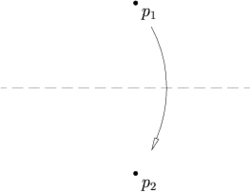
Правило 2

Пусть заданы две точки p₁ и p₂, тогда лист можно сложить так, что одна точка перейдёт в другую.

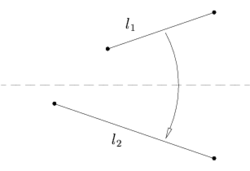
Правило 3

Пусть заданы две прямые l₁ и l₂, тогда лист можно сложить так, что одна прямая перейдёт в другую.

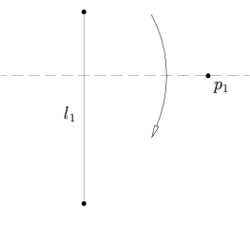
Правило 4

Пусть заданы прямая l₁ и точка p₁, тогда лист можно сложить так, что точка попадёт на складку, а прямая перейдёт сама в себя (т.е. линия складки будет ей перпендикулярна).

Правило 5

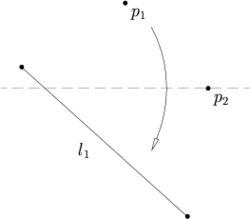
Пусть заданы прямая l₁ и две точки p₁ и p₂, тогда лист можно сложить так, что точка p₂ попадёт на складку, а p₁ на прямую l₁.

Правило 6

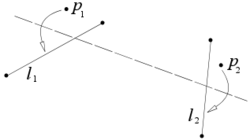
Пусть заданы две прямые l₁ и l₂ и две точки p₁ и p₂, тогда лист можно сложить так, что точка p₁ попадёт на прямую l₁, а точка p₂ попадёт на прямую l₂.

Правило 7

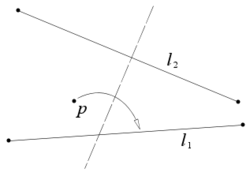
Пусть заданы две прямые l₁ и l₂ и точка p, тогда лист можно сложить так, что точка p попадёт на прямую l₁, а прямая l₂ прейдёт сама в себя (т.е. линия складки будет ей перпендикулярна).

Замечания

Все складки в этом списке можно получить как результат последовательного применения правила номер 6. То есть для математика они ничего не добавляют, однако позволяют уменьшить количество сгибов. Система из семи правил является полной, то есть они описывают все возможные способы получения одной новой складки на листе бумаги, путем совмещения уже существующих различных элементов листа. Это последнее утверждение было доказано Лэнгом^[1].

Возможные и невозможные построения

Все построения являются ничем иным, как решениями какого-либо уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа. В рамках вышеописанных требований, возможны следующие построения:

• Построение решений линейных уравнений.
• Построение решений квадратных уравнений.
• Построение решений кубических уравнений (правило 6).

Иначе говоря, возможно построить лишь числа равные арифметическим выражениям с использованием квадратного и кубического корней из исходных чисел (длин отрезков).

В частности, при помощи таких построений можно осуществить удвоение куба, трисекцию угла, построение правильного семиугольника. Решение задачи о квадратуре круга однако остаётся невозможным, так как π — трансцендентное число.

История

Основное правило (немер 6) было рассмотрено М. П. Белох^[2], ей же принадлежат первые построения трисекции угла и квадратуры круга с помощью оригами-построений . Полный список правил появляется в работе Жака Жустина^[3], который позднее также ссылался на Питера Мессера как на соавтора. Практически одновременно правила 1—6 были сформулированы Хамяки Худзита^[4]. Последнее седьмое правило добавил ещё позже Косиро Хатори^[5].

Вариации и обобщения

Список возможных построений можно значительно расширить, если позволить создание нескольких складок за один раз. Хотя человек, решивший провести несколько складок за одно действие на практике столкнется с трудностями физического порядка, тем не менее возможно вывести правила, аналогичные правилам Худзита и для этого случая^[6]. При допущении таких дополнительных правил, возможно доказать следующую теорему:

Любое алгебраическое уравнение степени n может быть решено n-2 одновременными складками

Представляет интерес, возможно ли решить то же уравнение складыванием, вовлекающим меньшее количество одновременных складок. Это, несомненно, верно для n=4 и неизвестно для n=5^[6].

См. также

Математика оригами

Литература

• А. Петрунин, Плоское оригами и построения.

По-английски

• Huzita Axiomas на сайте Роберта Лэнга
• T. Hull Origami Geometric Constructions

1. ↑ R. Lang Origami and Geometric Constructions
2. ↑ M. P. Beloch, Sul metodo del ripiegamento della carta per la risoluzione dei problemi geometrici, Periodico di Mathematiche, Ser. 4, Vol. 16, 1936, 104—108.
3. ↑ Justin, Jacques, Resolution par le pliage de l'equation du troisieme degre et applications geometriques, reprinted in Proceedings of the First International Meeting of Origami Science and Technology, H. Huzita ed. (1989), 251—261.
4. ↑ Humiaki Huzita, ”Axiomatic Development of Origami Geometry,” Proceedings of the First International Meeting of Origami Science and Technology, Humiaki Huzita, ed., 1989, pp 143–158.
5. ↑ Koshiro Hatori, Origami Construction
6. ↑ ^{1 2} Roger C. Alperin and Robert J. Lang, "One-, Two-, and Multi-Fold Origami Axioms.