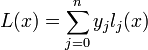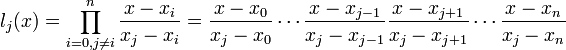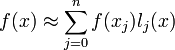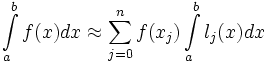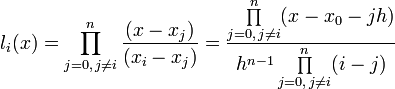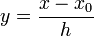- Полином Лагранжа
-
Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел
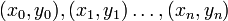 , где все xi различны, существует единственный многочлен L(x) степени не более n, для которого L(xi) = yi.
, где все xi различны, существует единственный многочлен L(x) степени не более n, для которого L(xi) = yi.В простейшем случае (n = 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.
Содержание
Определение
 Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы yj lj(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных xi
Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы yj lj(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных xiЛагранж предложил способ вычисления таких многочленов:
где базисные полиномы определяются по формуле:
lj(x) обладают следущими свойствами:
- являются многочленами степени n
- lj(xj) = 1
- lj(xi) = 0 при
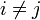
Отсюда следует, что L(x), как линейная комбинация lj(x), может иметь степень не больше n, и L(xj) = yj,
Применения
Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.
Пусть для функции f(x) известны значения yj = f(xj) в некоторых точках. Тогда мы можем интерполировать эту функцию как
В частности,
Значения интегралов от lj не зависят от f(x), и их можно вычислить заранее, зная последовательность xi.
Для случая равномерного распределения по отрезку узлов интерполяции
В указанном случае можно выразить xi через расстояние между узлами интерполяции h и начальную точку x0:
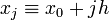 ,
,
и, следовательно,
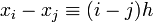 .
.
Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим
Теперь можно ввести замену переменной
и получить полином от y, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования алгоритмов с многобайтным представлением чисел.
Внешние ссылки
Wikimedia Foundation. 2010.