- Поверхность уровня
-
Если каждой точке M области многомерного пространства поставлено в соответствие некоторое (обычно — действительное) число u, то говорят, что в этой области задано скалярное поле. Другими словами, скалярное поле — это функция, отображающая Rn в R (скалярная функция).
Чаще других в приложениях встречаются:
- Функция трёх переменных:
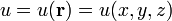 (пространственное поле).
(пространственное поле). - Функция двух переменных:
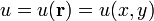 (плоское поле).
(плоское поле).
Обычно от скалярной функции требуется непрерывность или дифференцируемость достаточное количество раз (то есть функция должна принадлежать Cm).
Примеры пространственных скалярных полей: температура; электростатический потенциал. Пример плоского поля: глубина моря, отмеченная каким-либо образом на плоской карте.
- Обычно под скалярным полем понимается поле, инвариантное при преобразованиях координат (иногда, и нередко - при определенном классе преобразований координат, например, при преобразованиях, сохраняющих объем, ортогональных преобразованиях итп; но не менее редко имеется в виду инвариантность скалярного поля при произвольных преобразованиях координат, ограниченных, быть может, только гладкостью). (См. скаляр).
- В этом смысле далеко не каждая вещественнозначная функция координат является скалярным полем. Простейший пример: в этом смысле не является скалярным полем одна из координатных компонент векторного поля, так как при изменении выбора координат (например, при повороте координатных осей) она не останется неизменной (то есть не является инвариантом преобразований координат).
- Под скалярным полем в современной теоретической физике понимается (также и в особенности) обычно фундаментальное поле скаляра пространства Минковского (лоренц-инвариантное поле) или поле, инвариантное относительно общекоординатных преобразований, (обычно первое и второе практически совпадает).
- Практическими синонимами термина скалярное поле в смысле, обсуждаемом в данном параграфе, являются термины поле спина ноль частица спина ноль, скалярная частица (последние, всё же несколько разводя эти близкие понятия, называют также возбуждениями скалярного поля).
- Экспериментально (пока) не открыто ни одно фундаментальное скалярное (в смысле данного параграфа) поле. Однако такие поля играют немалую роль в теоретических построениях (существуют важные гипотетические скалярные поля, например, поле Хиггса), а также их наличие (наряду с векторными и тензорными полями, понимаемыми в том же смысле и наблюдаемыми реально) необходимо для полноты классификации фундаментальных полей.
Поверхность уровня
Скалярное поле можно представить графически с помощью поверхности уровня. Поверхностью уровня скалярного поля u = u(x,y,z) называется множество точек пространства, в которых функция u принимает одно и то же значение c, то есть поверхность уровня определяется уравнением u(x,y,z) = c.
Для плоского поля вместо поверхности получаются линии уровня. Примеры: изобата, изотерма и прочие изолинии.
Градиент
Направление скорейшего возрастания поля
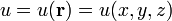 указывает вектор градиента
указывает вектор градиента 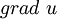 , или
, или 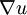 , с координатами:
, с координатами: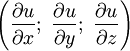 .
.
Градиент всегда перпендикулярен поверхностям уровня (в плоском поле — линиям уровня). Исключение - особые точки поля, в которых градиент равен нулю.
Литература
- Борисенко А. И., Тарапов И. Е. Векторный анализ и начала тензорного исчисления. 3-е изд. М.: Высшая школа, 1966.
- Гольдфайн И. А. Векторный анализ и теория поля. М.: Наука, 1968.
- Кочин Н. Е. Векторное исчисление и начала тензорного исчисления. 9-е изд. М.: Наука, 1965.
- Функция трёх переменных:
Wikimedia Foundation. 2010.
