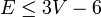- Планарность
-
Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.
Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины это точки плоскости, а ребра линии на ней, области, на которые граф разбивает поверхность называются гранями. Плоский граф — граф уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.
Содержание
Критерий непланарности
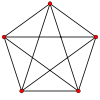 K5, полный граф с 5 вершинами
K5, полный граф с 5 вершинами K3,3, граф, иллюстрирующий задачу о трех колодцах
K3,3, граф, иллюстрирующий задачу о трех колодцах- достаточное условие — если граф содержит двудольный подграф K3,3 или полный подграф K5, то он является не планарным;
- необходимое условие — если граф не планарный, то он должен содержать больше 4 вершин, степень которых больше 3, или больше 5 вершин степени больше 2.
Теорема Понтрягина-Куратовского
Граф планарен тогда и только тогда, когда не содержит подграфов, гомеоморфных K5 или K3,3.
- Вариант
Граф планарен тогда и только тогда, когда он не содержит подграфов, стягиваемых в K5 или K3,3.
Формула Эйлера
Для связного плоского графа справедливо следующее соотношение между количеством вершин V, ребер E и граней F:
- V − E + F = 2
Оно было найдено Эйлером в 1736 г.[1] при изучении свойств выпуклых многогранников. Это соотношение справедливо и для других поверхностей с точностью до коэффициента, называемого эйлеровой характеристикой. Это инвариант поверхности, для плоскости или сферы он равен двум.
Формула имеет множество полезных следствий. Из того, что каждая грань ограничена не более чем тремя ребрами, следует, что для плоского графа
то есть, при большем числе ребер граф заведомо непланарен. (Обратное утверждение не верно, пример.) Отсюда следует, что в планарном графе всегда можно найти вершину степени не более 5.
Планарные графы в задачах
Задача о трех колодцах. Есть три дома и три колодца. Доказать, что невозможно так проложить дорожки между домами и колодцами, чтобы от каждого дома к каждому колодцу вела дорожка, и никакие две дорожки не пересекались бы. (Мосты строить нельзя.)
Раскраска карты. Необходимо раскрасить плоскую карту заданным числом красок так, что любые две страны имеющий общий участок границы имели различные цвета. Оказывается, что при отсутствии анклавов, всегда достаточно четырех красок, но это утверждение чрезвычайно сложно доказать, см. Проблема четырёх красок.
См. также
Примечания
- ↑ Ф. Харари Теория графов УРСС стр. 126
Ссылки
- А. Ю. Ольшанский. Плоские графы, СОЖ, 1996, No 11, с. 117—122.
- Ф. Харари. Теория графов. М.: «Мир». 1973
- ДИСКРЕТНАЯ МАТЕМАТИКА: АЛГОРИТМЫ, визуализация графов, апплеты
Wikimedia Foundation. 2010.