Гамма-алгоритм

Гамма-алгоритм

Гамма алгоритм — алгоритм плоской укладки графа и проверки его на планарность.

Определения

Плоский граф — это граф, нарисованный на плоскости таким образом, что его ребра не пересекаются.

Планарный граф — это граф, который изоморфен плоскому графу. То есть планарный граф — это граф с пересечениями, но допускающий его плоскую укладку.

Грань — это часть плоскости, окруженная простым циклом и не содержащая внутри себя других элементов графа.

Внешняя грань — это вся плоскость, окружающая плоский граф.

Алгоритм

На вход подаются графы, обладающие следующими свойствами:

1. граф связный;
2. граф имеет хотя бы один цикл;
3. граф не имеет мостиков, то есть ребер после удаления которых, граф распадается на две компоненты связности.

Если нарушено свойство (1), то граф нужно укладывать отдельно по компонентам связности. Если нарушено свойство (2), то граф — дерево и нарисовать его плоскую укладку тривиально. Случай нарушения свойства (3) рассмотрим более подробно. Если в графе есть мостики, то их нужно разрезать, провести отдельно плоскую укладку каждой компоненты связности, а затем соединить их мостиками. Здесь может возникнуть трудность: в процессе укладки концевые вершины мостика могут спрятаться внутри плоского графа. Нарисуем одну компоненту связности и будем присоединять к ней другие последовательно. Каждую новую компоненту связности будем рисовать в той грани, в которой лежит концевая вершина соответствующего мостика. Так как граф связности мостиками компонент связности является деревом, мы сумеем получить плоскую укладку.

Реализация

1. (Инициализация). Выберем любой простой цикл C исходного графа G; изобразим его на плоскости в виде грани, которую примем за уже уложенную часть G′; сформируем сегменты S_i; если множество сегментов пусто, то перейти к п. 3.
2. (Общий шаг). Пока множество сегментов не пусто:
   1. Для каждого сегмента S найти множество Γ(S). Если существует сегмент S, для которого |Γ(S)| = 0, то граф не планарный, конец.
   2. Выбираем один из сегментов с минимальным числом, вмещающих его граней.
   3. Выбираем одну из подходящих граней для выбранного сегмента.
   4. В данном сегменте выбираем цепь между двумя контактными вершинами и укладываем ее в выбранной грани. Учтем изменения в структуре сегментов и перейдем к п. a).
   5. (Завершение). Построена плоская укладка G′ исходного графа G, конец.

Каждый сегмент S относительно уже построенного графа G′ представляет собой одно из двух:

1. ребро, оба конца которого принадлежат G′, но само оно не принадлежит G′;
2. связную компоненту графа G — G′ дополненную всеми ребрами графа G, один из концов которых принадлежит связной компоненте, а второй из графа G′.

Те вершины, которые одновременно принадлежат G′ и какому-то сегменту назовем контактными. Если бы в каком-нибудь сегменте не было ни одной контактной вершины, то граф до разрезания был бы несвязный; если бы была только одна, то граф имел бы мостик. Эти возможности заранее исключены, так что каждый сегмент имеет не менее двух контактных вершин. Поэтому в каждом сегменте имеется цепь между любой парой таких вершин. Если все контактные вершины сегмента S имеют номера вершин какой-то грани Γ, то мы будем говорить, что грань Γ вмещает этот сегмент и обозначать S⊂Γ. Может быть имеется не одна такая грань, вмещающая сегмент S, множество таких граней обозначим Γ(S), а их число |Γ(S)|. На общем шаге мы обозреваем все сегменты S_i и определяем числа |Γ(S_i)|. Если хоть одно из них равно 0, то граф не планарен, конец. Иначе, выбираем сегмент, для которого число |Γ(S)| минимально, или один из множества, если таких сегментов несколько. В этом сегменте найдем цепь между двумя контактными вершинами и уложим ее в любую из граней множества Γ(S), совместив контактные вершины сегмента с соответствующими вершинами грани. При этом данная грань разобьется на две. Уже уложенная часть графа G′ по количеству ребер и вершин увеличится, а сегмент, из которого вынута цепь, исчезнет или развалится на меньшие с новыми контактными вершинами, ведущими к вершинам G′. Выбор подходящей грани для выбранного сегмента реализуется так: находим общую грань для контактных вершин. Если таковая существует, то грань считается подходящей; в противном случае контактные вершины лежат в разных гранях, а значит цепь, соединяющая их, пересечет как минимум 1 сегмент и граф не будет планарен.

Корректность гамма-алгоритма

Вначале докажем ряд вспомогательных утверждений.

Лемма 1

Для любого сегмента |Γ(S)| ≤ 2.

Доказательство: Действительно, если все контактные вершины одного сегмента принадлежат некоторой грани Γ (точнее, циклу, окружающему эту грань), то они могут принадлежать все вместе только одной еще грани, а именно внутренней или внешней. Ч. т. д. Назовем сегменты S1 и S2 конфликтующими относительно уже уложенной части, если: существует грань, которая вмещает каждый из сегментов; в сегментах S1 и S2 есть две цепи (между контактными вершинами) L1 и L2 соответственно, такие, что их невозможно уложить в одну грань без пересечения.

Лемма 2

Конфликтующие сегменты S1 и S2 обладают следующим свойством: если |Γ(S1)| = 2 и |Γ(S2)| = 2, то Γ(S1) = Γ(S2).

Доказательство: Действительно, в противном случае, имея по определению одну общую вмещающую грань Γ3, они бы имели еще по собственной вмещающей грани Γ1 и Γ2 соответственно. Тогда любые цепи из S1 и S2 могли бы разместиться в Γ1 и Γ2 соответственно, а значит и в Γ3, причем без пересечения; следовательно, S1 и S2 не были бы конфликтующими. Противоречие. Лемма доказана.

Замечание Из доказанной леммы следует, что, имея сегмент S1, и еще сегмент S2, конфликтующий с S1, затем сегмент S3, конфликтующий с S2 (но не с S1) и т. д., причем каждый вмещается в две грани, то эти грани общие для всех сегментов последовательности, и можно размещать цепь L1 из S1 в первую грань Γ1, L2 из S2 в Γ2, L3 из S3 снова в Γ1 и т. д. до конца последовательности. Если цепочка сегментов замыкается в цикл четной длины, то проблем не будет; если в нечетный цикл, то в конце окажется, что два конфликтующих сегмента нужно разместить без пересечений в общую грань, что невозможно.

Теорема Кёнига

В графе все циклы четные тогда и только тогда, когда граф является двудольным.

Доказательство: Достаточность. Рассмотрим двудольный граф. Начнем цикл в верхней доли. Нужно пройти по четному числу ребер, чтобы подняться снова в верхнюю долю. Следовательно, при замыкании цикла число ребер будет четным.
Необходимость. Если граф несвязный, то проведем доказательство отдельно для каждой компоненты. Пусть граф связный и все циклы в нем четные. Выделим произвольную вершину v₀ и найдем произвольные цепи между v₀ и всеми остальными вершинами (например, самые короткие алгоритмом Дейкстры). Если одна цепь (v₀, v_i) нечетной длины, то и любая цепь (v₀, v_i) нечетная, иначе бы эти цепи образовали нечетный цикл. Аналогично, если (v₀, v_i) — четная, то и любая (v₀, v_i) — четная. Разобьем вершины на две доли: в одну войдет вершина v₀ и все, находящиеся от v₀ на четном расстоянии; в другую долю поместим все вершины, находящиеся от v₀ на нечетном расстоянии. Если вершины u₁ и u₂ принадлежат одной доле, то между ними не может быть ребра, иначе это ребро вместе с цепями (v₀, u₁) и (v₀, u₂) образовали бы нечетный цикл. Ч. т. д.

Частичной укладкой G′ планарного графа G называется граф, который можно получить из какой-нибудь укладки графа G на плоскости удалением каких-то ребер и вершин. Таким образом, частичная укладка — это правильное начало укладки, в ней ещё не сделано ошибок.

В частичной укладке G′ сопоставим каждому сегменту вершину в некотором постороннем служебном графе A(G′), где вершины соединяются ребрами, если соответствующие сегменты являются конфликтующими.

Лемма 3

Если результатом некоторого шага работы гамма-алгоритма является частичная укладка G′ планарного графа G такая, что |Γ(S)| = 2 для любого сегмента S относительно G′, то A(G′) — двудольный граф.

Доказательство:Пусть A(G′) — не двудольный, тогда по теореме Кенига в нем есть цикл нечетной длины. По Лемме 2 все вершины этого цикла вмещаются ровно двумя гранями. Поскольку цикл нечетный, мы не сможем уложить эти сегменты в две грани. Противоречие. Лемма доказана.

Используя доказанные выше утверждения, докажем корректность Гамма-алгоритма.

Теорема

Гамма-алгоритм корректен, то есть, если G — планарный граф, то результатом каждого шага гамма-алгоритма является частичная укладка G′.

Доказательство: Докажем индукцией по числу шагов.

База индукции: результат инициализации есть плоская укладка, так как уложенный цикл будет в любой укладке.
Шаг индукции: Пусть граф G'_{k − 1}, полученный на (k−1)-м шаге, является частичной укладкой. На текущем шаге к нему присоединится цепь L: G'_k = G'_{k − 1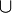} $\cup$ L. Докажем, что граф G'_k— тоже частичная укладка. Среди сегментов на текущем шаге нет такого S, что |Γ(S)| = 0, иначе G'_{k − 1} не был бы частичной укладкой. Значит, либо существует S такой, что |Γ(S)| = 1, либо все S таковы, что |Γ(S)| = 2. Первый случай означает, что укладка S в Γ неизбежна, так что граф G'_k после добавления цепи из S останется частичной укладкой. Во втором случае построим граф A (G'_{k − 1}), по Лемме 3 он двудольный. Возьмем его связную компоненту A′, этот граф тоже двудольный. Для сегментов из A′ имеются ровно две грани Γ1 и Γ2, вмещающие их. Раскидаем сегменты A′ по граням Γ1 и Γ2 попеременно. Это необходимо сделать в каждой частичной укладке, следовательно получена частичная укладка. Фактически, основой последней части доказательства было, что если граф A (G'_{k − 1}) — двудольный, то после удаления части ребер и вершин граф A (G'_k) тоже двудольный. Таким образом, в результате каждой итерации для планарного графа частичная укладка увеличивается, в конце мы получим плоскую укладку.

Литература

• Бондарев В.М., Рублинецкий В.И., Качко Е.Г. Основы программирования.. — Харьков: Фолио, 1997.
• Харари Ф. Теория графов.. — Москва: Мир, 1973.

См. также

• Словарь терминов теории графов
• Теория графов
• Дискретная математика