Параболоиды

Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (т.е. не имеющая центра симметрии) поверхность второго порядка.

Канонические уравнения параболоида в декартовых координатах:

z = ax² + by²

• если a и b одного знака, то параболоид называется эллиптическим.
• если a и b разного знака, то параболоид называется гиперболическим.
• если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.

Эллиптический параболоид

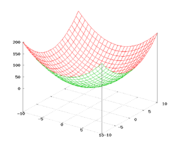Эллиптический параболоид при a=b=1

Эллипти́ческий параболо́ид — поверхность, описываемая функцией вида

$~2z = x^2/a^2 + y^2/b^2$,

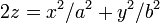где a и b одного знака. Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.

Если a = b то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину данной параболы.

Гиперболический параболоид

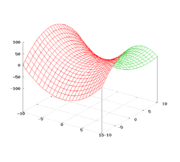Гиперболический параболоид при a=b=1

Гиперболи́ческий параболо́ид (называемый в строительстве «гипар») — седлообразная поверхность, описываемая в прямоугольной системе координат уравнением вида

$z = \frac {x^2}{a^2} - \frac {y^2}{b^2}=\left(\frac xa+\frac yb\right)\left(\frac xa-\frac yb\right)$.

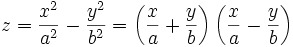Из второго представления видно, что гиперболический параболоид является линейчатой поверхностью.

Поверхность может быть образована движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается со второй своей вершиной.

Параболоиды в мире

В технике

Антенна

В искусстве

В литературе

Устройство, описанное в Гиперболоид инженера Гарина должно было быть параболоидом.