ПАРАБОЛОИДЫ — незамкнутые поверхности (2 го порядка). Параболоид может быть образован движением параболы, вершина которой скользит по другой, неподвижной параболе (с осью, параллельной оси движущейся параболы), тогда как ее плоскость, смещаясь параллельно… … Большой Энциклопедический словарь
параболоиды — незамкнутые поверхности (2 го порядка). Параболоид может быть образован движением параболы, вершина которой скользит по другой, неподвижной параболе (с осью, параллельной оси движущейся параболы), тогда как её плоскость, смещаясь параллельно… … Энциклопедический словарь
ПАРАБОЛОИДЫ — незамкнутые поверхности (2 го порядка). П. может быть образован движением параболы, вершина к рой скользит по другой, неподвижной параболе (с осью, параллельной оси движущейся параболы), тогда как её плоскость, смещаясь параллельно самой себе,… … Естествознание. Энциклопедический словарь
Параболоиды — Параболоид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (т.е. не имеющая центра симметрии) поверхность второго порядка. Канонические уравнения параболоида в декартовых координатах: z = ax2 … Википедия
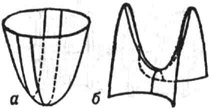
Параболоиды — (от Парабола и греч. éidos вид) незамкнутые поверхности второго порядка, не имеющие центра. Различают два вида П.: эллиптический П. (рис. 1) и гиперболический П. (рис. 2). П. представляют собой два типа из общего числа пяти основных типов … Большая советская энциклопедия
Поверхности второго порядка — поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2 й степени: a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0 (*) Уравнение (*)… … Большая советская энциклопедия
Радиотелескоп — РТФ 32 Обсерватория «Зеленчукская» Северный Кавказ Радиотелескоп … Википедия
Поверхность — (Surface, Oberfläche). Всякую непрерывную кривую линию можно представить, как след движущейся точки. Подобно этому и всякую П. можно образовать или описать движением в пространстве некоторой кривой линии неизменяемого или изменяемого вида и… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ОБОЛОЧКА — твёрдое деформируемое тело, ограниченное двумя криволинейными поверхностями, расстояние между к рыми мало по сравнению с двумя др. размерами. Оболочки разл. формы: а цилиндрич. оболочка кругового сечения; б коническая; в сферическая; г… … Физическая энциклопедия
ПОВЕРХНОСТЬ ВТОРОГО ПОРЯДКА — множество точек 3 мерного действительного (или комплексноро) пространства, координаты к рых в декартовой системе удовлетворяют алгебраич. уравнению 2 й степени (*) Уравнение (*) может и не определять действительного геометрич. образа, в таких… … Математическая энциклопедия