Поверхность второго порядка

Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

$a_{11}x^2 + a_{22}y^2+a_{33}z^2+2a_{12}xy+2a_{23}yz+2a_{13}xz+2a_{14}x+2a_{24}y+2a_{34}z+a_{44}=0$

в котором по крайней мере один из коэффициентов $a_{11}$, $a_{22}$, $a_{33}$, $a_{12}$, $a_{23}$, $a_{13}$ отличен от нуля.

Типы поверхностей второго порядка

Цилиндрические поверхности

Поверхность $S$ называется цилиндрической поверхностью с образующей $\vec{l}$, если для любой точки $M_0$ этой поверхности прямая, проходящая через эту точку параллельно образующей $\vec{l}$, целиком принадлежит поверхности $S$.

Теорема (об уравнении цилиндрической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность $S$ имеет уравнение $f(x,y)=0$, то $S$ — цилиндрическая поверхность с образующей, параллельной оси $OZ$.

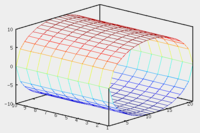
Кривая, задаваемая уравнением $f(x,y)=0$ в плоскости $z=0$, называется направляющей цилиндрической поверхности.

Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.

Эллиптический цилиндр:	Параболический цилиндр:	Гиперболический цилиндр:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\!$	$y^2=2px\!$	$\frac{x^2}{a^2}-\frac{y^2}{b^2}\!=1$
Пара совпавших прямых:	Пара совпавших плоскостей:	Пара пересекающихся плоскостей:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=0\!$	$y^2=0\!$	$\frac{x^2}{a^2}-\frac{y^2}{b^2}\!=0$

Конические поверхности

Коническая поверхность.

Основная статья: Коническая поверхность

Поверхность $S$ называется конической поверхностью с вершиной в точке $O$, если для любой точки $M_0$ этой поверхности прямая, проходящая через $M_0$ и $O$, целиком принадлежит этой поверхности.

Функция $F(x,y,z)$ называется однородной порядка $m$, если $\forall t \in \mathbb{R}\;\forall x,y,z$ выполняется следующее: $F(tx,ty,tz)=t^mF(x,y,z)\!$

Теорема (об уравнении конической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность $S$ задана уравнением $F(x,y,z)=0$, где $F(x,y,z)$ — однородная функция, то $S$ — коническая поверхность с вершиной в начале координат.

Если поверхность $S$ задана функцией $F(x,y,z)$, являющейся однородным алгебраическим многочленом второго порядка, то $S$ называется конической поверхностью второго порядка.

• Каноническое уравнение конуса второго порядка имеет вид:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0\!$

Поверхности вращения

Поверхность $S$ называется поверхностью вращения вокруг оси $OZ$, если для любой точки $M_0(x_0,y_0,z_0)$ этой поверхности окружность, проходящая через эту точку в плоскости $z=z_0$ с центром в $(0,0,z_0)$ и радиусом $r=\sqrt{x_0^2+y_0^2}$, целиком принадлежит этой поверхности.

Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность $S$ задана уравнением $F(x^2+y^2,z)=0$, то $S$ — поверхность вращения вокруг оси $OZ$.

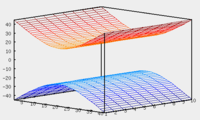
Эллипсоид:	Однополостной гиперболоид:	Двуполостной гиперболоид:	Эллиптический параболоид:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\!$	$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1\!$	$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1\!$	$\frac{x^2}{a^2}+\frac{y^2}{b^2}=2pz\!$

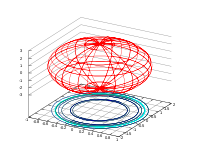
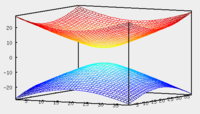
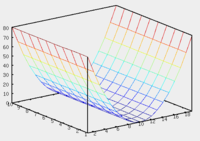
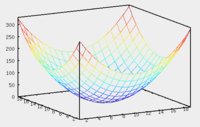
В случае, если $a=b\neq 0$, перечисленные выше поверхности являются поверхностями вращения.

Эллиптический параболоид

Уравнение эллиптического параболоида:

$\frac {x^2}{a^2} + \frac {y^2}{b^2} = 2pz$

Если $a=b$ то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину и фокус данной параболы.

При сечении эллиптический параболоида плоскостью $z=z_0$ поверхность порождает эллипс.

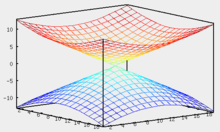
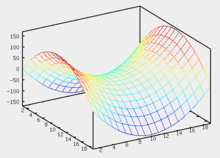
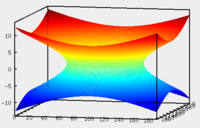
При сечении эллиптический параболоида плоскостью $x=x_0$ или $y=y_0$ поверхность порождает параболу.

Гиперболический параболоид

Гиперболический параболоид.

Уравнение гиперболического параболоида:

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=2pz\!$

При сечении гиперболического параболоида плоскостью $z=z_0$ поверхность порождает гиперболу.

При сечении гиперболического параболоида плоскостью $x=x_0$ или $y=y_0$ поверхность порождает параболу.

Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».

Центральные поверхности

Если центр поверхности второго порядка существует и единственен, то его координаты $\left(x_0,\;y_0\;z_0\right)$ можно найти решив систему уравнений:

$\begin{cases} a_{11}x_0 + a_{12}y_0 + a_{13}z_0 + a_{14} = 0 \\ a_{21}x_0 + a_{22}y_0 + a_{23}z_0 + a_{24} = 0 \\ a_{31}x_0 + a_{32}y_0 + a_{33}z_0 + a_{34} = 0 \end{cases}$

Литература

• В. А. Ильин, Э. Г. Позняк. Аналитическая геометрия.. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
• П. С. Александров. Курс аналитической геометрии и линейной алгебры.. — М.: ФИЗМАТЛИТ, 1979. — 511 с.
• Шаль. Исторический обзор происхождения и развития геометрических методов. Гл. 5, § 46-54. М., 1883.

См. также

• Квадрика
• Поверхность вращения
• Цилиндрическая поверхность
• Гиперболоид
• Параболоид
• Эллипсоид