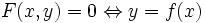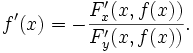Неявная функция

Теорема о неявной функции — общее название для теорем, гарантирующих локальное существование и описывающих свойства неявной функции, т. е. функции

y = f(x),   $f:X\to Y$,

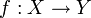заданной уравнением

F(x,y) = z₀,   $F:X\times Y\to Z$

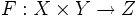
и значение 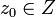$z_0\in Z$ фиксированно.

Одномерный случай

Простейшая теорема о неявной функции состоит в следующем.

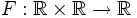
Если функция $F:\R\times\R\to\R$ непрерывна в некоторой окрестности точки (x0,y0) F(x0,y0) = 0 и При фиксированном x, функция F(x,y) строго монотонна по y в данной окрестности, тогда найдётся такой двумерный промежуток 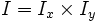$I=I_x \times I_y$, являющийся окрестностью точки (x0,y0), и такая непрерывная функция 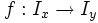$f:I_x\to I_y$, что для любой точки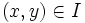 $(x,y) \in I$ $F(x,y) = 0 \Leftrightarrow y = f(x)$

Обычно дополнительно предполагается что функция F непрерывно дифференцируема, в этом случае условие монотнности следует из того что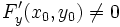 $F_y'(x_0,y_0)\ne0\quad$, здесь F_y' обозначает частную производную F по y. Более того, в этом случае, производная функции f может быть вычислена по формуле

$f'(x) = - \frac{F_x'(x, f(x))}{F_y'(x, f(x))}.$

Многомерный случай

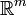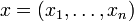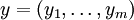Пусть $\R^n$ и $\R^m$ суть n- и m-мерные евклидовы пространства с фиксированными системами координат, точки которых соответственно $x=(x_1,\dots,x_n)$ и $y=(y_1,\dots,y_m)$. Пусть F отображает некоторую окрестность W точки 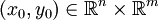$(x_0,y_0)\in\R^n\times\R^m$ в пространство 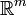$\R^m$ и F₁,F₂,...,F_m — координатные функции (от переменных 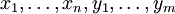$x_1,\dots,x_n,y_1,\dots,y_m$) отображения F, т. е. F = (F₁,F₂,...,F_m).

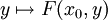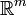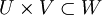Если отображение F дифференцируемо на W, F(x₀,y₀) = 0, а якобиан отображения $y\mapsto F(x_0,y)$ не равен нулю в y₀ то существуют окрестности U и V точек x₀ и y₀ соответственно в пространствах $\R^n$ и $\R^m$, $U\times V\subset W$ и единственное отображение 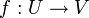$f : U \to V$ такие, что для всех 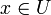$x\in U$ выполняется условие $F(x, f(x)) = 0\in \R^m$.

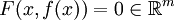При этом f(x₀) = y₀. Более того, отображение f дифференцируемо на U.

Литература

• Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981;
• Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965;
• Никольский С. М., Курс математического анализа, 2 изд., т. 1—2, М., 1975;
• Шварц Л., Анализ, пер. с франц., т. 1, М., 1972;
• Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971.