- НЕЯВНАЯ ФУНКЦИЯ
- функция
 заданная уравнением
заданная уравнением 
 - нек-рые множества, т. е. такая функция f, что при любом
- нек-рые множества, т. е. такая функция f, что при любом 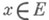 имеет место
имеет место  . Если
. Если  - топологич. пространства и для нек-рой точки
- топологич. пространства и для нек-рой точки  выполняется условие
выполняется условие  то при определенных условиях в нек-рой окрестности точки
то при определенных условиях в нек-рой окрестности точки  уравнение
уравнение 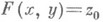 однозначно разрешимо относительно одной из переменных. Свойства решения этого уравнения описываются теоремами о Н. ф.
однозначно разрешимо относительно одной из переменных. Свойства решения этого уравнения описываются теоремами о Н. ф.Простейшая теорема о Н. ф. состоит в следующем. Пусть Xи Y - подмножества числовой прямой
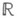 ,
,  - внутренняя точка множества
- внутренняя точка множества  на плоскости; тогда если функция Fнепрерывна в нек-рой окрестности точки
на плоскости; тогда если функция Fнепрерывна в нек-рой окрестности точки  и существуют такие
и существуют такие  что при любом фиксированном
что при любом фиксированном  функция
функция 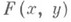 как функция переменного устрого монотонна на интервале
как функция переменного устрого монотонна на интервале
 , то найдется такое
, то найдется такое  , что существует и притом единственная функция
, что существует и притом единственная функция  такая, что
такая, что  для всех
для всех  причем функция f(х)непрерывна и
причем функция f(х)непрерывна и  . Условия этой теоремы выполняются, если функция
. Условия этой теоремы выполняются, если функция  непрерывна в окрестности точки
непрерывна в окрестности точки 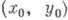 , существует частная производная Fy , непрерывная в точке
, существует частная производная Fy , непрерывная в точке  ,
, 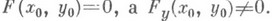 Если, кроме того, существует и частная производная
Если, кроме того, существует и частная производная 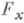 , также непрерывная в точке
, также непрерывная в точке  то Н. ф. f дифференцируема в точке x0 , причем
то Н. ф. f дифференцируема в точке x0 , причем 
Эта теорема обобщается на случай системы уравнений, т. е. когда Fявляется векторной функцией. Пусть
 и
и 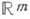 суть
суть 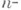 и
и  мерные евклидовы пространства с фиксированными системами координат, точки к-рых соответственно
мерные евклидовы пространства с фиксированными системами координат, точки к-рых соответственно  Пусть Fотображает нек-рую окрестность Wточки
Пусть Fотображает нек-рую окрестность Wточки 
 в пространство
в пространство  и
и 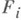 ,
,  - координатные функции (от n+m переменных
- координатные функции (от n+m переменных  отображения F, т. е.
отображения F, т. е.
 . Если отображение Fдифференцируемо на
. Если отображение Fдифференцируемо на  а якобиан
а якобиан
то существуют окрестности Uи Vточек х 0 и у 0 соответственно в пространствах
 и единственное отображение
и единственное отображение  такие, что для всех
такие, что для всех 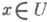 выполняется условие
выполняется условие  . При этом
. При этом  отображение f дифференцируемо на U, а если
отображение f дифференцируемо на U, а если 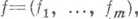 то явное выражение для частных производных
то явное выражение для частных производных  находится из системы т. линейных относительно этих производных уравнений
находится из системы т. линейных относительно этих производных уравнений
k=1, 2, ..., т, i фиксировано (i=l, 2, ..., п). Иногда основное утверждение теоремы формулируется следующим образом: существуют окрестности Uи W0 точек х 0 и
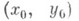 в пространствах
в пространствах 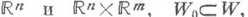 и единственное отображение
и единственное отображение 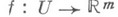 такие, что для всех
такие, что для всех  выполняются условия
выполняются условия  ,
, 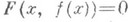 . Иначе говоря, условия
. Иначе говоря, условия  равносильны условиям
равносильны условиям 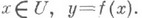 В этом случае говорят, что уравнение F(x, y)=0 однозначно разрешимо в окрестности W0 точки ( х 0 , у 0 ).
В этом случае говорят, что уравнение F(x, y)=0 однозначно разрешимо в окрестности W0 точки ( х 0 , у 0 ).Сформулированная класcич. теорема о Н. ф. обобщается на случай более общих пространств следующим образом. Пусть X - топологич. пространство, Y и Z- аффинные нормированные пространства над полем действительных или комплексных чисел, т. е. аффинные пространства над указанными полями, к-рым сопоставлены соответственно нормированные векторные пространства
 причем
причем  - полное пространство,
- полное пространство, 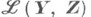 - множество линейных непрерывных отображений пространства
- множество линейных непрерывных отображений пространства  в пространство
в пространство 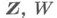 - открытое множество в произведении пространств
- открытое множество в произведении пространств  и
и 
Пусть
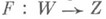 - непрерывное отображение
- непрерывное отображение 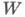 в
в  Если при каждом фиксированном хи
Если при каждом фиксированном хи  отображение Fимеет частную Фреше произ водную
отображение Fимеет частную Фреше произ водную , причем
, причем  является непрерывным отображением
является непрерывным отображением  а линейное отображение
а линейное отображение  имеет непрерывное обратное линейное отооражение (т. е. является обратимым элементом пространства
имеет непрерывное обратное линейное отооражение (т. е. является обратимым элементом пространства  ), то существуют такие открытые соответственно в пространствах Xи Y множества
), то существуют такие открытые соответственно в пространствах Xи Y множества  что для любого
что для любого  существует и притом единственный элемент
существует и притом единственный элемент  , обозначаемый
, обозначаемый 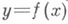 и удовлетворяющий условиям:
и удовлетворяющий условиям:
При этом так определенная функция
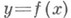 является непрерывным отображением Uв Vи
является непрерывным отображением Uв Vи  .
.Если Xтакже является аффинным нормированным пространством, то при определенных условиях Н. ф.
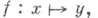 удовлетворяющая уравнению
удовлетворяющая уравнению
также дифференцируема. Именно, пусть X, Y, Z- аффинные нормированные пространства, W- открытое множество из

 и пусть f - неявное отображение, задаваемое уравнением (1) и отображающее нек-рую окрестность Uточки х 0 в открытое подмножество Vпространства
и пусть f - неявное отображение, задаваемое уравнением (1) и отображающее нек-рую окрестность Uточки х 0 в открытое подмножество Vпространства  Таким образом, для всех
Таким образом, для всех  имеет место
имеет место
Пусть, кроме того, отображение f непрерывно в точке х 0 и
 . Тогда если отображение Fдифференцируемо в точке
. Тогда если отображение Fдифференцируемо в точке 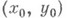 и его частные производные Фреше
и его частные производные Фреше  и
и  являются линейными непрерывными операторами, отображающими соответственно векторные пространства
являются линейными непрерывными операторами, отображающими соответственно векторные пространства  , сопоставленные аффинным пространствам Xи Y, в векторное пространство
, сопоставленные аффинным пространствам Xи Y, в векторное пространство  , сопоставленпое аффинному пространству Z, причем оператор Fy(x0 , y0 )является обратимым элементом пространства
, сопоставленпое аффинному пространству Z, причем оператор Fy(x0 , y0 )является обратимым элементом пространства  , то отображение f дифференцируемо в точке х 0 и его производная Фреше задается формулой
, то отображение f дифференцируемо в точке х 0 и его производная Фреше задается формулой
Эта формула получается в результате формального дифференцирования функции (2):

и умножения слева этого равенства на
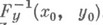 .
. Если, кроме того, отображение
 непрерывно дифференцируемо на W, Н. ф.
непрерывно дифференцируемо на W, Н. ф. непрерывна на
непрерывна на  и для любого
и для любого  частная производная Фреше Fy(x, f(x))является обратимым элементом пространства .
частная производная Фреше Fy(x, f(x))является обратимым элементом пространства . , то отображение f - непрерывно дифференцируемое отображение Uв V.
, то отображение f - непрерывно дифференцируемое отображение Uв V.Можно указать и в общем случае условия существования и единственности Н. ф. в терминах непрерывности производной Фреше: если пространство Zполно, отображение
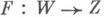 непрерывно дифференцируемо на
непрерывно дифференцируемо на  и частная производная Фреше Fy(x0, y0) является обратимым элементом пространства
и частная производная Фреше Fy(x0, y0) является обратимым элементом пространства 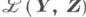 , то уравнение (1) однозначно разрешимо в достаточно малой окрестности точки ( х 0, у 0), т. е. существуют окрестности Uи Vточек х 0 и у 0 соответственно в пространствах Xи Y,
, то уравнение (1) однозначно разрешимо в достаточно малой окрестности точки ( х 0, у 0), т. е. существуют окрестности Uи Vточек х 0 и у 0 соответственно в пространствах Xи Y,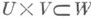 и единственная Н. ф.
и единственная Н. ф.  удовлетворяющая условиям (2). При этом отображение f непрерывно дифференцируемо на U. В таком виде теорема о Н. ф. для нормированных пространств представляет собой прямое обобщение соответствующей классич. теоремы о Н. ф. для одного скалярного уравнения с двумя переменными.
удовлетворяющая условиям (2). При этом отображение f непрерывно дифференцируемо на U. В таком виде теорема о Н. ф. для нормированных пространств представляет собой прямое обобщение соответствующей классич. теоремы о Н. ф. для одного скалярного уравнения с двумя переменными.Если, кроме того, функция
 непрерывно дифференцируема в окрестности Wточки
непрерывно дифференцируема в окрестности Wточки  раз (k=1, 2, ...), то Н. ф.
раз (k=1, 2, ...), то Н. ф. также краз непрерывно дифференцируема.
также краз непрерывно дифференцируема.Более далекие обобщения классич. теоремы о Н. ф. на случай дифференциальных операторов даны Дж. Нэшем (J. Nash) (см. Наша теорема).
Лит.:[1] Колмогоров А. Н., Фомин С. В., Элементы теории функции и функционального анализа, 5 изд., М., 1981; [2] Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1905; [3] Никольский С. М., Курс математического анализа, 2 изд., т. 1-2, М., 1975; [4] Шварц Л., Анализ, пер. с франц., т. 1, М., 1972; [5] Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971.
Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
