- НЕЯВНАЯ ФУНКЦИЯ
в алгебраической геометрии - функция, задаваемая алгебраич. уравнением. Пусть
 - многочлен от
- многочлен от  (напр., с комплексными коэффициентами). Тогда многообразие
(напр., с комплексными коэффициентами). Тогда многообразие  нулей этого многочлена можно рассматривать как график нек-рого соответствия
нулей этого многочлена можно рассматривать как график нек-рого соответствия 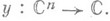 Это соответствие н называют, допуская известную неточность, функцией, неявно заданной уравнением
Это соответствие н называют, допуская известную неточность, функцией, неявно заданной уравнением  Вообще говоря, соответствие умногозначное и не всюду определенное и поэтому не является функцией в обычном смысле. Имеется два способа превратить это соответствие в функцию. Первый, восходящий к Б. Риману (В. Riemann), заключается в том, что областью определения Н. ф. усчитают не
Вообще говоря, соответствие умногозначное и не всюду определенное и поэтому не является функцией в обычном смысле. Имеется два способа превратить это соответствие в функцию. Первый, восходящий к Б. Риману (В. Riemann), заключается в том, что областью определения Н. ф. усчитают не  , а многообразие V(F), конечнолистно накрывающее
, а многообразие V(F), конечнолистно накрывающее 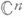 . Этот прием приводит к очень содержательному понятию римановой поверхности. При таком подходе понятие Н. ф. смыкается с понятием алгебраической функции.
. Этот прием приводит к очень содержательному понятию римановой поверхности. При таком подходе понятие Н. ф. смыкается с понятием алгебраической функции.Другой способ состоит в том, чтобы представить V(Р)локально как график однозначной функции. Различные теоремы о Н. ф. утверждают существование открытых
 и
и  для к-рых
для к-рых  является графиком гладкой в том или ином смысле функции
является графиком гладкой в том или ином смысле функции  (см. Неявная функция). Однако открытые подмножества Uи W, как правило, не являются открытыми в топологии Зариского и лишены смысла в абстрактной алгебраич. геометрии. Поэтому указанный способ модифицируется следующим образом. Формальным ростком (или ветвью) в точке
(см. Неявная функция). Однако открытые подмножества Uи W, как правило, не являются открытыми в топологии Зариского и лишены смысла в абстрактной алгебраич. геометрии. Поэтому указанный способ модифицируется следующим образом. Формальным ростком (или ветвью) в точке  Н. ф., заданной уравнением
Н. ф., заданной уравнением 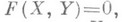 наз. формальный степенной ряд
наз. формальный степенной ряд  такой, что F(X, y) = 0. Вообще, степенной ряд у, удовлетворяющий полиномиальному уравнению
такой, что F(X, y) = 0. Вообще, степенной ряд у, удовлетворяющий полиномиальному уравнению  наз. алгебраическим степенным рядом. Алгебраический степенной ряд сходится в некоторой окрестности точки а.
наз. алгебраическим степенным рядом. Алгебраический степенной ряд сходится в некоторой окрестности точки а.Пусть А- локальное нётерово кольцо с максимальным идеалом m. Элемент уиз пополнения
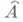 локального кольца Аназ. алгебраическим над А, если
локального кольца Аназ. алгебраическим над А, если  для нек-рого многочлена
для нек-рого многочлена  . Множество алгебраических над
. Множество алгебраических над  элементов
элементов  образует кольцо
образует кольцо  Следующий вариант теоремы о Н. ф. показывает, что алгебраич. функций достаточно много. Пусть
Следующий вариант теоремы о Н. ф. показывает, что алгебраич. функций достаточно много. Пусть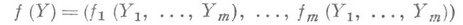
- набор тмногочленов из
 и пусть
и пусть 
 - элементы поля вычетов
- элементы поля вычетов  такие, что:
такие, что:1)
 (черта сверху означает редукцию по модулю m);
(черта сверху означает редукцию по модулю m);2)
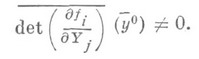
Тогда существуют алгебраические над А элементы
 такие, что
такие, что  Другими словами, А- гензелево кольцо.
Другими словами, А- гензелево кольцо.Другой результат того же типа - теорема Артина об аппроксимации (см. [2]). Пусть А-локальное кольцо, являющееся локализацией алгебры конечного типа над полем. Пусть, далее, задана система
 полиномиальных уравнений с коэффициентами из А(или нз
полиномиальных уравнений с коэффициентами из А(или нз  ) и
) и  - вектор с коэффициентами из пополнения
- вектор с коэффициентами из пополнения  такой, что
такой, что  Тогда найдется вектор
Тогда найдется вектор  с коэффициентами из
с коэффициентами из  , сколь угодно близкий к
, сколь угодно близкий к  и такой, что
и такой, что  Вариант этой теоремы верен [3] и для систем аналитич. равнений.
Вариант этой теоремы верен [3] и для систем аналитич. равнений.Лит.:[1] Ар тин М., "Успехи матем. наук", 1971, т. 26, в. 1, с. 181-205; [2] Art in M., "Publ. Math. IHES", 1969, № 36, р. 23-58; [3] его же, "Invent, math.", 1968, v. 5, p. 277 - 91.
В. И. Данилов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
