Возвратное состояние — Возвратное состояние это состояние марковской цепи, посещаемое ею бесконечное число раз. Содержание 1 Определение 2 Критерий возвратности 3 … Википедия
Существенное состояние — Существенное состояние это такое состояние цепи Маркова, покинув которое, она всегда может в него вернуться. Определение Пусть дана однородная цепь Маркова с дискретным временем и дискретным пространством состояний . Тогда состояние… … Википедия
Периодическое состояние — Периодическое состояние это такое состояние цепи Маркова, которое навещается цепью только через промежутки времени, кратные фиксированному числу. Период состояния Пусть дана однородная цепь Маркова с дискретным временем с матрицей… … Википедия
Достижимое состояние — Определение Пусть однородная цепь Маркова с дискретным временем. Состояние называется достижимым из состояния , если существует такое, что . Пишут … Википедия
АКЦИДЕНЦИЯ — (лат. accidentia, от accidere случаться). 1) посторонний доход, прибыль. 2) особенного рода пошлина, в виде штрафа за неправильно показанный товар, провезенный чрез таможню. 3) несущественное, случайное. 4) производство мелких типографских работ … Словарь иностранных слов русского языка
ПАРЕТО — (Pareto) Вильфредо (1848 1923) ит. социолог и экономист. Все поступки делятся П. на логические и нелогические. В категорию нелогических поступков попадают те действия, которые субъективно или объективно не обнаруживают логической связи. В первой… … Философская энциклопедия
Возвратная цепь Маркова — Возвратное состояние это состояние Марковской цепи, посещаемое ею бесконечное число раз. Содержание 1 Определение 2 Критерий возвратности 3 Время возвращения … Википедия
ПСИХОЛОГИЯ — наука о психической реальности, о том, как индивид ощущает, воспринимает, чувствует, мыслит и действует. Для более глубокого понимания человеческой психики психологи исследуют психическую регуляцию поведения животных и функционирование таких… … Энциклопедия Кольера
Цепь Маркова — Пример цепи с двумя состояниями Цепь Маркова последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, го … Википедия
Маркова цепь — Цепь Маркова последовательность случайных событий с конечным или счётным бесконечным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Названа в честь А. А. Маркова … Википедия
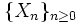 и дискретным пространством состояний
и дискретным пространством состояний 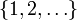 . Тогда состояние i называется несуще́ственным, если существует состояние j и
. Тогда состояние i называется несуще́ственным, если существует состояние j и 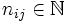 , такие что
, такие что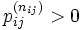 , но
, но 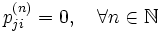 .
. .
.