- Неразложимый класс
-
Определение
Пусть
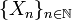 — однородная цепь Маркова с дискретным временем. Состояние j называется достижи́мым из состояния i, если существует n = n(i,j) такое, что
— однородная цепь Маркова с дискретным временем. Состояние j называется достижи́мым из состояния i, если существует n = n(i,j) такое, что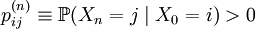 .
.
Пишут
 .
.Сообщающиеся состояния
- Состояния i и j называются сообща́ющимися, если
 и
и 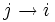 . Пишем:
. Пишем:  .
.
- Свойство сообщаемости порождает на пространстве состояний отношение эквивалентности. Порождаемые классы эквивалентности называются неразложи́мыми кла́ссами. Если цепь Маркова такова, что её состояния образуют лишь один неразложимый класс, то она называется неразложи́мой.
- Состояния, принадлежащие одному и тому же неразложимому классу, либо все возвратные, либо все невозвратные. Таким образом неразложимый класс целиком либо возвратен, либо невозвратен. Наконец, неразложимая цепь Маркова либо целиком возвратна, либо целиком невозвратна.
Примеры
- Пусть
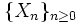 - цепь Маркова с тремя состояниями {1,2,3}, и её матрица переходных вероятностей имеет вид
- цепь Маркова с тремя состояниями {1,2,3}, и её матрица переходных вероятностей имеет вид
Состояния этой цепи образуют два неразложимых класса: {1,2} и {3}. В частности,
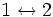 , но
, но 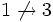 и
и 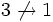 .
.- Цепь Маркова, задаваемая матрицей переходных вероятностей
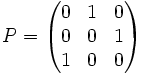 ,
,
неразложима.
Классификация состояний и цепей Маркова Состояние: апериодическое | возвратное | достижимое | невозвратное | несущественное | нулевое | периодическое | положительное | сообщающееся | существенное Цепь: апериодическая | возвратная | невозвратная | неразложимая | нулевая | периодическая | положительная | разложимая | эргодическая
Wikimedia Foundation. 2010.

