Момент остановки

Марковский момент времени в теории случайных процессов - это случайная величина, не зависящая от будущего рассматриваемого случайного процесса.

Дискретный случай

Определение

Пусть дана последовательность случайных величин 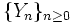$\{Y_n\}_{n \ge 0}$. Тогда случайная величина τ называется марковским моментом (времени), если для любого $n \ge 0$ событие $\{\tau \le n\}$ зависит только от случайных величин $Y_0,\ldots, Y_n$.

Пример

Пусть 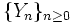$\{Y_n\}_{n \ge 0}$ - последовательность независимых нормальных случайных величин. Пусть $L \in \mathbb{R}$, и

$\tau = \inf \{ n \ge 0 \mid Y_n \ge L \}$

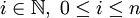- момент первого достижения процессом {Y_n} уровня L. Тогда τ - марковский момент, ибо $\tau \le n$ тогда и только тогда, когда существует $i\in \mathbb{N},\; 0 \le i \le n$ такое, что $Y_i \ge L$. Таким образом событие $\{\tau \le n\}$ зависит лишь от поведения процесса до момента времени n.

Пусть теперь

$\sigma = \sup \{ n \ge 0 \mid Y_n \ge L \}$

- момент последнего достижения процессом {Y_n} уровня L. Тогда σ не является марковским моментом, ибо событие $\{\sigma \le n\}$ предполагает знание поведения процесса в будущем.

Общий случай

Определения

• Пусть дано вероятностное пространство 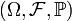$(\Omega,\mathcal{F},\mathbb{P})$ с фильтрацией $\{\mathcal{F}_t\}_{t \in T}$, где $T \subset [0, \infty)$. Тогда случайная величина τ принимающая значения в $T \cup \{\infty\}$ называется марковским моментом относительно данной фильтрации, если $\{ \tau \le t \} \in \mathcal{F}_t,\quad \forall t \in T$.

• Если дан процесс 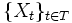$\{X_t\}_{t \in T}$, и $\mathcal{F}_t = \sigma (X_s \mid s \le t)$ - его естественные σ-алгебры, то говорят, что τ - марковский момент относительно процесса {X_t}.

• Марковский момент называется моментом остановки, если он конечен почти наверное, то есть

$\mathbb{P}(\tau < \infty) = 1$.

Свойства

Если τ и σ - марковские моменты, то

• τ + σ - марковский момент;
• $\tau \wedge \sigma \equiv \min(\tau, \sigma)$ - марковский момент;
• $\tau \vee \sigma \equiv \max(\tau, \sigma)$ - марковский момент.

Замечание

Момент остановки может не иметь конечного математического ожидания.

Пример

Пусть $\{W_t\}_{t \ge 0}$ - стандартный винеровский процесс. Пусть α > 0. Определим

$\tau = \inf \{t \ge 0 \mid W_t \ge \alpha \}$.

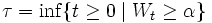Тогда τ - марковский момент, имеющий распределение, задаваемое плотностью вероятности

$f_{\tau}(t) = \frac{\alpha}{\sqrt{2 \pi t^3}}e^{-\frac{\alpha^2}{2t}},\quad t \ge 0$.

В частности τ - момент остановки. Однако,

$\mathbb{E} \tau = \infty$.