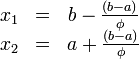- Метод чисел Фибоначчи
-
Метод золотого сечения — метод поиска значений действительно-значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации.
Содержание
Описание метода
Пусть задана функция
![f(x):\;[a,\;b]\to\mathbb{R},\;f(x)\in\mathrm{C}([a,\;b])\!](/pictures/wiki/files/101/e82e4b18dd5c512108a74eea6389d09e.png) . Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки
. Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки  и
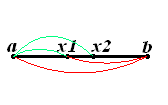
и 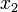 такие, что:Иллюстрация выбора промежуточных точек метода золотого сечения.
такие, что:Иллюстрация выбора промежуточных точек метода золотого сечения.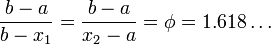 , где
, где 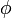 — пропорция золотого сечения.
— пропорция золотого сечения.
Таким образом:
То есть точка
 делит отрезок
делит отрезок ![[a,\;x_2]\!](/pictures/wiki/files/57/9742f662f5ca40b5c3c490deabf5837d.png) в отношении золотого сечения. Аналогично
в отношении золотого сечения. Аналогично 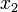 делит отрезок
делит отрезок ![[x_1,\;b]\!](/pictures/wiki/files/51/3cb3f38d9bfec96035c744c7516b052a.png) в той же пропорции. Это свойство и используется для построения итеративного процесса.
в той же пропорции. Это свойство и используется для построения итеративного процесса.Алгоритм
На первой итерации заданный отрезок делится двумя симметричными относительно его центра, точками и рассчитываются значения в этих точках. После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поиска минимума), отбрасывают. На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку. Процедура продолжается до тех пор, пока не будет достигнута заданная точность.
Формализация
- Шаг 1. Задаются начальные границы отрезка
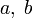 и точность
и точность 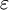 , рассчитывают начальные точки деления:
, рассчитывают начальные точки деления: 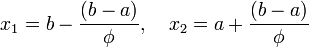 и значения в них целевой функции:
и значения в них целевой функции: 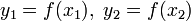 .
. - Шаг 2.
- Если
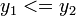 , то
, то 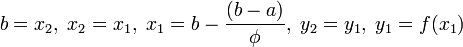 .
. - Иначе
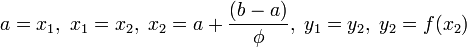 .
.
- Если
- Шаг 3.
- Если
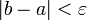 , то
, то 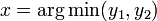 и останов.
и останов. - Иначе возврат к шагу 2.
- Если
Метод чисел Фибоначчи
В силу того, что в асимптотике
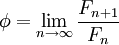 , метод золотого сечения может быть трансформирован в так называемый метод чисел Фибоначчи. Однако при этом в силу свойств чисел Фибоначчи количество итерации строго ограничено. Это удобно, если сразу задано количество возможных обращений к функции.
, метод золотого сечения может быть трансформирован в так называемый метод чисел Фибоначчи. Однако при этом в силу свойств чисел Фибоначчи количество итерации строго ограничено. Это удобно, если сразу задано количество возможных обращений к функции.Алгоритм
- Шаг 1. Задаются начальными границами отрезка
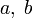 и числом итераций
и числом итераций 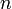 , рассчитывают начальные точки деления:
, рассчитывают начальные точки деления: 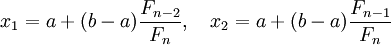 и значения в них целевой функции:
и значения в них целевой функции: 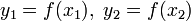 .
. - Шаг 2.
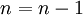 .
.
- Если
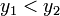 , то
, то 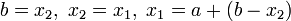 .
. - Иначе
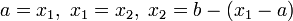 .
.
- Если
- Шаг 3.
- Если
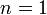 , то
, то 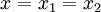 и останов.
и останов. - Иначе возврат к шагу 2.
- Если
Литература
- Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. пец. вузов. — М.: Высш. шк., 1986.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
- Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
См. также
Wikimedia Foundation. 2010.