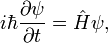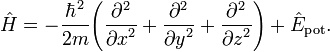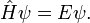Математическое основание квантовой механики

Математический аппарат нерелятивистской квантовой механики строится на следующих положениях:^[1]

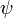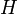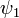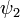• Чистые состояния системы описываются ненулевыми векторами $~\psi$ комплексного сепарабельного гильбертова пространства $~H$, причем векторы $~\psi_1$ и $~\psi_2$ описывают одно и то же состояние тогда и только тогда, когда 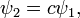$~\psi_2=c\psi_1 ,$ где $~c$ — произвольное комплексное число. Каждой наблюдаемой однозначно сопоставляется линейный самосопряженный оператор.
• Наблюдаемые одновременно измеримы тогда и только тогда, когда соответствующие им самосопряженные операторы перестановочны (коммутируют).
• Эволюция чистого состояния гамильтоновой системы во времени определяется нестационарным уравнением Шредингера

$~i\hbar\frac{\partial \psi}{\partial t}= \hat{H}\psi ,$

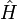где $~\hat{H}$ — гамильтониан:

$~{\hat{H}}=-{\frac{{\hbar}^2}{2m}}{ \left( {\frac{{{\partial}^2}{}}{{{\partial}x}^2}}+{\frac{{{\partial}^2}{}}{{{\partial}y}^2}}+{\frac{{{\partial}^2}{}}{{{\partial}z}^2}} \right) }+{\hat E_{\rm{pot}}} .$

Стационарные, т.е. не меняющиеся со временем состояния, определяются стационарным уравнением Шредингера:

$~{{\hat{H}}{\psi}}={E{\psi}} .$

• Каждому вектору 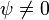$~\psi\not=0$ из пространства 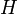$~H$ отвечает некоторое чистое состояние системы, любой линейный самосопряженный оператор соответствует некоторой наблюдаемой.

Эти положения позволяют создать математический аппарат, пригодных для описания широкого спектра задач в квантовой механике гамильтоновых систем, находящихся в чистых состояниях. Дальнейшим развитием этого аппарата является уравнение Дирака, которое с хорошей точностью позволяет описать релятивистские эффекты. Для описания состояний открытых, негамильтоновых и диссипативных квантовых систем используется матрица плотности, а для описания эволюции таких систем применяется уравнение Линдблада.

Литература

• Боголюбов Н. Н., Логунов А. А., Тодоров И. Т. Основы аксиоматического подхода в квантовой теории поля. М.: Наука, 1969. 424с.
• Боголюбов Н. Н., Логунов А. А., Оксак А. И., Тодоров И. Т. Общие принципы квантовой теории поля. М.: Наука, 1987. 616с.
• Браттели У., Робинсон Д. Операторные алгебры и квантовая статистическая механика. М.: Мир, 1982. 512с.
• Дж. фон Нейман Математические основы квантовой механики, М.: Наука 1964.
• Эмх Ж. Алгебраические методы в статистической механике и квантовой теории поля. М.: Мир, 1976. 424с.
• Холево А. С. Вероятностные и статистические аспекты квантовой теории. М.: Наука, 1980. 320с.
• Холево А. С. Статистическая структура квантовой теории. Москва, Ижевск: РХД 2003. 188с.

Ссылки

1. ↑ Ф. А. Березин, М. А. Шубин. Уравнение Шредингера. — М.: Изд-во Моск. ун-та, 1983.