- Интерполяционная формула
-
Интерполяционные формулы, формулы, дающие приближённое выражение функции
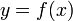 при помощи интерполяции, то есть через интерполяционный многочлен
при помощи интерполяции, то есть через интерполяционный многочлен 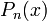 степени
степени 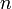 , значения которого в заданных точках
, значения которого в заданных точках 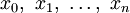 совпадают со значениями
совпадают со значениями 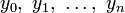 функции
функции 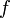 в этих точках. Многочлен
в этих точках. Многочлен 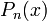 определяется единственным образом, но в зависимости от задачи его удобно записывать различными по виду формулами.
определяется единственным образом, но в зависимости от задачи его удобно записывать различными по виду формулами.Содержание
Интерполяционная формула Лагранжа
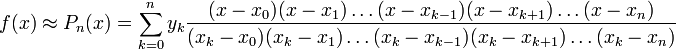
Ошибка, совершенная при замене функции выражением
выражением 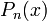 , не превышает по абсолютной величине
, не превышает по абсолютной величине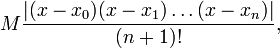
где —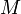 — максимум абсолютной величины
— максимум абсолютной величины 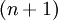 -й производной
-й производной 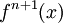 функции
функции  на отрезке
на отрезке 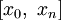 .
.Интерполяционная формула Ньютона
см. Интерполяционные формулы Ньютона
Если точки
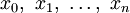 расположены на равных расстояниях
расположены на равных расстояниях 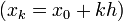 , многочлен
, многочлен 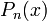 можно записать так:
можно записать так: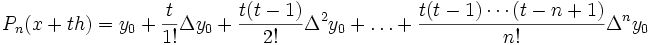
(здесь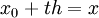 , а
, а 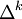 — разности k-го порядка:
— разности k-го порядка: 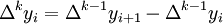 ). Это так называемая формула Ньютона для интерполирования вперёд; название формулы указывает на то, что она содержит заданные значения
). Это так называемая формула Ньютона для интерполирования вперёд; название формулы указывает на то, что она содержит заданные значения 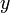 , соответствующие узлам интерполяции, находящимся только вправо от
, соответствующие узлам интерполяции, находящимся только вправо от 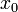 . Эта формула удобна при интерполировании функций для значений
. Эта формула удобна при интерполировании функций для значений 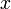 , близких к
, близких к 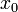 . При интерполировании функций для значений
. При интерполировании функций для значений 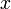 , близких к
, близких к 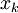 , формулу Ньютона целесообразно преобразовать, изменив начало отсчёта (см. ниже формулы Стирлинга и Бесселя).
, формулу Ньютона целесообразно преобразовать, изменив начало отсчёта (см. ниже формулы Стирлинга и Бесселя).
Формулу Ньютона можно записать и для неравноотстоящих узлов, прибегая для этой цели к разделённым разностям. В отличие от формулы Лагранжа, где каждый член зависит от всех узлов интерполяции, любой k-й член формулы Ньютона зависит от первых (от начала отсчёта) узлов и добавление новых узлов вызывает лишь добавление новых членов формулы (в этом преимущество формулы Ньютона).Короткая форма интерполяционной формулы Ньютона для случая равноудаленных узлов:
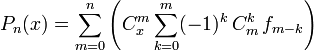
где
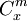 - обобщенные на область действительных чисел биномиальные коэффициенты.
- обобщенные на область действительных чисел биномиальные коэффициенты.Интерполяционная формула Стирлинга
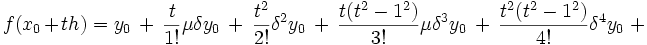
![\ + \ \frac{t(t^2-1^2)(t^2-2^2)}{5!} \mu \delta^5 y_0 \ + \ \cdots \ + \ \frac{t^2(t^2-1^2)(t^2-2^2) \cdots [t^2-(k-1)^2]}{(2k)!} \delta^{2k} y_0](/pictures/wiki/files/56/86bed1c956971961d28932dc8a995468.png)
(о значении символа
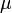 и связи центральных разностей
и связи центральных разностей 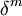 с разностями
с разностями 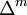 см. Конечных разностей исчисление) применяется при интерполировании функций для значений
см. Конечных разностей исчисление) применяется при интерполировании функций для значений 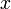 , близких к одному из средних узлов
, близких к одному из средних узлов 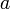 ; в этом случае естественно взять нечётное число узлов
; в этом случае естественно взять нечётное число узлов 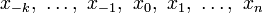 , считая
, считая 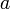 центральным узлом
центральным узлом 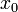 .
.Интерполяционная формула Бесселя
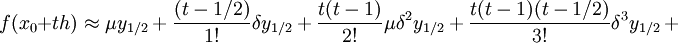
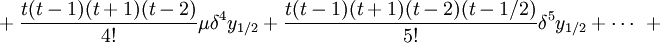
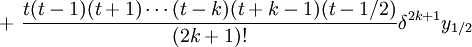
применяется при интерполировании функций для значений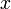 , близких середине
, близких середине 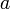 между двумя узлами; здесь естественно брать чётное число узлов
между двумя узлами; здесь естественно брать чётное число узлов 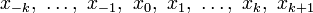 , и располагать их симметрично относительно
, и располагать их симметрично относительно 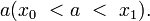
См. также
Ссылки
Литература
- Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954;
Wikimedia Foundation. 2010.
