ТОЧНО РЕШАЕМЫЕ МОДЕЛИ

ТОЧНО РЕШАЕМЫЕ МОДЕЛИ

к в а н т о в о й т е о р и и п о л я и с т а т и с т и ч е с к о й ф и з и к и (вполне интегрируемые системы), матем. модели физ. систем, допускающие точное вычисление собств. функций и собств. значений гамильтониана таких систем, а также статистич. суммы для них; как правило, это системы низкой пространственной размерности (одно- или двумерные; см., напр., Двумерные модели квантовой теории поля). Т. р. м. имеют принципиальное значение в физике фазовых переходов.

XYZ- м о д е л ь. Одной из фундаментальных Т. р. м. является одномерная квантовая анизотропная XYZ-модель Гейзенберга - периодическая цепочка N спинов ¹/₂, в к-рой учитывается только обменное взаимодействие ближайших соседей. Гамильтониан XYZ- моделизаписывается в виде (см. также Спиновый гамильтониан):

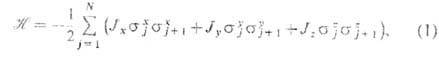
где 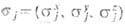-трёхмерный вектор, составленый из матриц Паули для j -го спина, J_a - константы анизотропного обменного взаимодействия (a = x,у,z); для частных значений констант J_a модель XYZ сводится к более простым точно решаемым моделям.

1. М о д е л ь И з и н г а 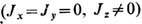точно решается, напр., методом трансфер-матрицы, или матрицы переноса (см. ниже), не только для обменного взаимодействия, но и в более общем случае при включении в гамильтониан внеш. магн. поля Н; этот метод также оказывается весьма полезным при решении ряда других Т. р. м.

Свободная энергия модели Изинга определяется наибольшим из двух собств. значений трансфер-матрицы. Однако при T=H=0оба собств. значения совпадают, обращая при этом корреляц. длину в бесконечность. Это означает, что в одномерной модели Изинга точка Т=Н=0. является критической точкой. Полученный результат есть следствие общей теоремы теории фазовых переходов, согласно к-рой дальний порядок (см. Дальний и ближний порядок )в системе возникает только тогда, когда наибольшее собств. значение трансфер-матрицы асимптотически вырождено. Такое поведение согласуется также с тем, что для одномерных систем с взаимодействием конечного радиуса вклад в свободную энергию от энтропийного слагаемого преобладает, и упорядоченное состояние оказывается термодинамически неустойчивым. В случае же с бесконечным радиусом взаимодействия собств. значения трансфер-матрицы становятся вырожденными, что соответствует фазовому переходу. Каждый спин системы при этом взаимодействует со всеми остальными спинами, так что вся цепочка представляет собой единый кластер, т. е. модель преобразуется в решётку с бесконечным координац. числом (т. <н. бесконечномерная модель), для к-рой точным оказывается среднего поля приближение.

Несмотря на чрезвычайную простоту, модель Изинга позволяет продемонстрировать два очень существ. факта для теории фазовых переходов: во-первых, одномерные системы имеют критич. точку, в к-рой темп-pa Т и магн. поле Н равны нулю, и, во-вторых, критические показатели физ. величин вблизи критич. точки удовлетворяют гипотезе подобия.

2. XY -м о д е л ь 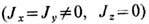сводится к другой Т. р. <м.- знаменитой двумерной модели Изинга, точное решение к-рой в 1944 нашёл Л. Онсагер (L. Onsager) (см. Изинга модель).

3. ХХХ- модель(J_x = J_y = J_z = J)- изотропная модель Гейзенберга. Решение получено Г. Бете в 1931 [I]. Использованный им метод решения в дальнейшем получил назв. а н з а т ц или п о д с т а н о в к а Б е т е. Следуя этому методу, рассмотрим состояние цепочки с m спинами, ориентированными вниз, и N-m спинами, ориентированными вверх. Пусть x₁<x₂<...<x_N- координаты узлов со спинами вниз 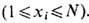Произвольная волновая ф-ция Ф _т с заданным полным спином, т. е. с определённым числом т спинов, ориентированных вниз, должна быть суперпозицией всех состояний | х₁...х _m>. с конкретным указанием узлов x₁,...,x_m, в к-рых располагаются ориентированные вниз спины:

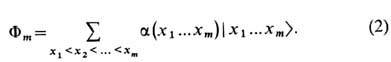
Суммирование здесь ведётся по всем разл. способам размещения т номеров по N узлам. Коэф. 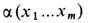можно найти, действуя на Ф _m гамильтонианом 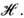Решение представляется в виде

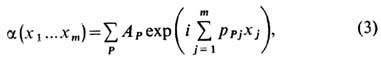
где р₁..., р _т - нек-рая совокупность неравных чисел, а Р - произвольная перестановка этих m чисел. Амплитуды А _р связаны с амплитудой A₀ = А₁₂... _т, отвечающей тождественной перестановке, соотношением

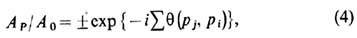
где суммирование q-факторов ведётся по всем парам индексов у амплитуды, к-рые необходимо транспонировать, чтобы прийти к правильной расстановке индексов, т. е. к амплитуде A₀ (j и i -индексы конкретной транспонируемой пары). Знак в (4) определяется чётностью или нечётностью перестановки Р. Фазовый q-фактор имеет вид

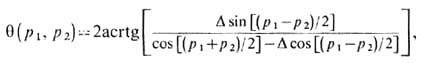
где

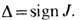
Собств. значение гамильтониана, соответствующее ф-ции Ф _т, записывается в виде

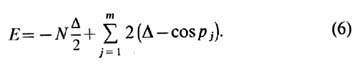
Числа р _i, характеризующие собств. значения и собств. ф-ции гамильтониана, представляют собой квазиимпульсы, и для их определения необходимо учесть граничные условия, выражающие тождественность состояния на узле х и N+x, т. е. замыкание цепочки. В результате система ур-ний на числа р₁...,р _т примет вид

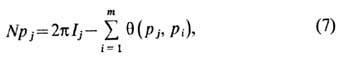
где для m чётных I_j- полуцелые, а для т нечётных I_j- целые числа. Дальнейший анализ ур-ний зависит от знака обменного взаимодействия J.

Для J>0, отвечающему ферромагн. осн. состоянию, Бете нашёл собств. ф-ции гамильтониана и определил спектр элементарных возбуждений. Ими оказались спиновые волны и m -частичные спиновые комплексы (связанные состояния m перевёрнутых спинов в ферромагн. цепочке). Однако наиб. успех в XXX -модели достигнут в случае антифер-ромагн. цепочки (J<0), для к-рой этим методом вычислена энергия осн. состояния и найден спектр элементарных возбуждений.

4. XXZ -м о д е л ь (J_x = J_y), или модель Гейзенберга - Изинга, точно решается методом анзатца Бете и сводится к двумерной, т. <н. ш е с т и в е р ш и н н о й, м о д е л и, к-рая, в свою очередь, известна также как модель типа льда на квадратной решётке (см. Двумерные решёточные модели). Связь этих моделей позволяет использовать результаты, полученные для шестивершинной модели в случае XXZ- модели. Преимущество классич. двумерной шестивершинной модели перед одномерной квантовой XXZ -моделью заключается в том, что для решения двумерной модели удобно использовать метод трансфер-матрицы.

5. А н и з о т р о п н а я XYZ -м о д е л ь связана с другой классич. двумерной моделью на квадратной решётке, а именно с восьмивершинной моделью. Точное решение классич. двумерной восьмивершинной модели - крупнейшее достижение в области точно решаемых моделей - получено в 1972 Р. Бакстером [2]. Он обнаружил противоречие с гипотезой универсальности и независимости критич. показателей от деталей взаимодействия. Решение восьмивершинной модели позволило вычислить энергию осн. состояния и найти спектр элементарных возбуждений XYZ -модели.

Т. о., основополагающей идеей метода исследования точно решаемых одномерных квантовых систем является анзатц Бете (с соответствующим усложнением при переходе к более сложным моделям). С матем. точки зрения точное решение восьмивершинной модели потребовало нетривиального обобщения анзатца Бете. Бакстер установил фундам. соотношение для факторизованной трёхча-стичной матрицы рассеяния, к-рое сейчас известно как ур-ние Янга - Бакстера (см. ниже). Общность и содержательность этого ур-ния особенно проявилась в создании в 1979 Л. Д. Фаддеевым и его сотрудниками [3] к в а нт о в о г о м е т о д а о б р а т н о й з а д а ч и (КМОЗ)-алгеб-раич. варианта анзатца Бете. КМОЗ является естеств. развитием классич. обратной задачи рассеяния метода, к-рый позволил найти обширный класс двумерных нелинейных эволюционных ур-ний, имеющих точное решение.

Уравнение Янга - Бакстера. Изотропная модель Гейзен-берга является простейшей системой, точное решение к-рой достигается методом анзатца Бете, т. е. представлением волновой ф-ции в виде (3) и (4). Для этой модели рассматривается система взаимодействующих частиц (спиновых отклонений), к-рые не имеют внутр. структуры, и их состояние целиком задаётся их положением в цепочке (координатой); взаимодействие таких частиц сводится лишь к обмену импульсами. В то же время существует немало физ. задач, где состояние отражает и внутр. структуру частиц, т. е. характеризуется нек-рым дискретным индексом а, напр. проекцией спина. При взаимодействии друг с другом такие частицы могут не только обмениваться импульсами, но и менять свой дискретный индекс. Это обстоятельство требует обобщения анзатца Бете.

Рассмотрим систему из N частиц. Пусть 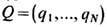и P=(p₁,...,p_N)- перестановки целых чисел 1, ..., N. Обобщённый анзатц Бете состоит в том, что волновая ф-ция системы 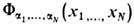для области

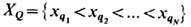
взаимной расстановки координат частиц имеет вид

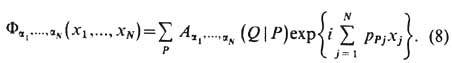
Ф-ции A(Q|P) разл. областей связаны между собой через S -матрицу. Если области 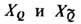отличаются друг от друга перестановкой i и j частиц, то эту связь в общем виде можно записать в виде соотношения

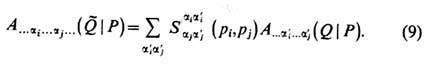
Величина 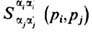наз. двухчастичной матрицей рассеяния. Используя многократно правило (9) для перестановки одной пары частиц, мы можем любую перестановку свести к тождественной перестановке 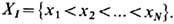Ко-эф. 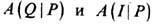будут связаны соотношением, в к-ром стоит произведение S -матриц, отвечающих всем транспозициям пары индексов, к-рые нужно сделать для сведения перестановки 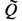к I. Т. о. возникает многочастичная матрица рассеяния, к-рая оказывается мультипликативной.

Между элементами двухчастичной матрицы рассеяния существует соотношение, играющее центр. роль в теории квантовых одномерных систем. Это соотношение следует из эквивалентности двух возможностей трёхчастичного процесса рассеяния. Используя такую параметризацию импульсов 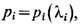при к-рой матрица рассеяния S(p₁,p₂ )будет ф-цией разности б ы с т р о т l₁ и l₂, S(l₁-l₂), соотношение для факторизованной трехчастичнои матрицы можно записать в виде

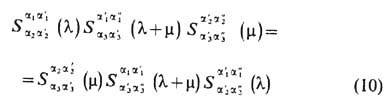
(по повторяющимся индексам подразумевается суммирование). Подобного типа соотношения при точном решении конкретных одномерных задач были получены в 1967 Ч. Янгом [4] и в 1972 Бакстером и наз. у р а в н е н и я м и Я н г а-Б а к с т е р а, а параметр 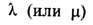наз. с п е к тр а л ь н ы м п а р а м е т р о м.

Квантовый метод обратной задачи. В этом методе одним из центральных объектов является т р а н с ф е р-м а тр и ц а T. Она определяется следующим образом:

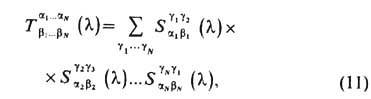
где 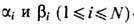-два набора чисел, каждый из к-рых может пробегать все l значений дискретного индекса a(или 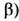. Такая искусств. конструкция T -матрицы размерности l^N полезна тем, что проблема диагонализации гамильтониана задачи сводится к отысканию собств. значений этой матрицы, что может представить выполнимую задачу.

Запишем трансфер-матрицу в инвариантной форме, перейдя от S -матрицы размерности l к нек-рой 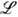-матрице размерности l^N+1 , следующим образом:

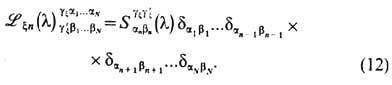
В многомерном пространстве эта матрица диагональна по всем индексам 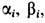кроме i = n. Выражение для T -матрицы в таком случае записывается в виде следа от произведения 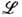-матриц, взятого только по вспомогат. матричным индексам g_x и g'_x:

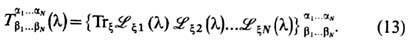
В операторной форме

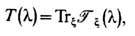
где

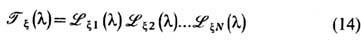
наз. м а т р и ц е й м о н о д р о м и и; её размерность равна l^{N + 1}.

Соотношение (10) для S -матриц можно переписать в терминах 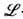-матриц, вводя матрицу 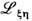ф-лой

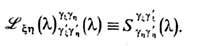
Тогда имеет место следующее ур-ние:

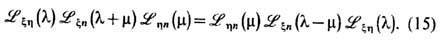
Отсюда следует аналогичное ур-ние для матрицы монодромии:

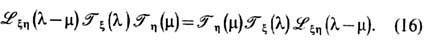
Ур-ния (15) и (16) удобно переписать в др. форме, если подействовать на них оператором перестановки 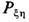индексов x и h :

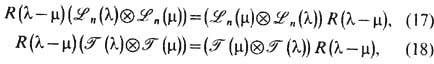
где введена 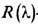-матрица размерности l²,

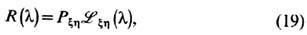
и символ тензорного произведения 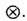Все ур-ния (15) - (18) также наз. ур-ниями Янга - Бакстера. Для ранее введённых T -матрицы и матрицы монодромии также справедливы ур-ния Янга - Бакстера. Дальнейшая программа состоит в том, чтобы установить связь этих матриц с гамильтонианом системы и провести их диагонализацию. Эта программа и составляет содержание КМОЗ и может быть фактически реализована только для конкретной системы. Проиллюстрируем технику КМОЗ на примере анизотропной гейзенберговской цепочки (XYZ -модели).

Для исследования системы с гамильтонианом (1) выберем в качестве двухчастичной матрицы рассеяния выражение

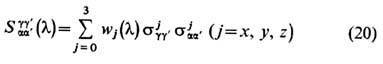
с разл. величинами w_j (суммирование по j ведётся по четырём индексам: j=x, у, z и 0, причём s⁰ представляет собой единичную двухрядную матрицу). Матричная запись S -матрицы будет следующей:

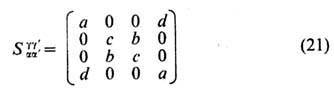
где

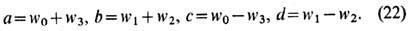
Записав с помощью выражения для S -матрицы локальные 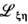-матрицы и R -матрицу, из ур-ния Янга-Бакстера находим систему ур-ний для определения величин 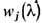. Для XYZ -мoдeли решение этой системы ур-ний приводит к следующей эллиптич. параметризации для коэф. матрицы рассеяния:

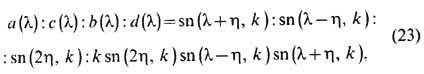
где k - модуль эллиптич. синуса. Величины h и k параметризуют две независимые константы гамильтониана (1). Эта параметризация выражается эллиптич. ф-циями Якоби

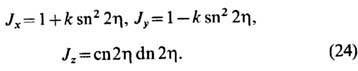
В частном случае k=0 получаем 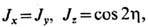т. <е. переходим к XYZ -модели, при этом эллиптич. параметризация переходит в тригонометрическую.

Установив зависимость элементов матрицы рассеяния от спектрального параметра l, можно убедиться, что в точке l=0 S -матрица совпадает с матрицей перестановки. Если с помощью этого частного значения S -матрицы образовать трансфер-матрицу по ф-ле (11), то именно через неё будут выражаться гамильтониан и импульс системы.

Сформулируем теперь общую схему квантового метода обратной задачи. Она состоит в двукратном использовании ур-ний Янга-Бакстера. На первом этапе решается ур-ние (17) в локальной форме и находится параметризация элементов матрицы рассеяния S(l) т. е. их зависимость от спектрального параметра l. На втором этапе используется ур-ние Янга - Бакстера в форме (18), из к-poro получаются коммутац. соотношения для матрицы монодромии. С их помощью производится диагонализа-ция трансфер-матрицы и находятся в явном виде её собств. значения. Гамильтониан системы и импульс выражаются через трансфер-матрицу, поэтому её диагонализация означает и диагонализацию гамильтониана, т. е., точнее, решение задачи.

Иллюстрирование схемы КМОЗ на примере XYZ -моде-ли показало, что для этой задачи было необходимо ввести S -матрицы вида (20). Существенно отметить, что для этой задачи введённая S -матрица не является физической, но представляет нек-рую абстрактную S -матрицу, использование к-рой в схеме КМОЗ приводит к диагонализации гейзенберговского гамильтониана. Для др. физ. задач, напр. о цепочке Хаббарда или об эффекте Кондо, частицы имеют внутр. симметрию и их состояния характеризуются дискретным индексом, конкретно - проекцией спина, поэтому физ. S- матрица в этих задачах является матрицей по этим индексам. Она должна удовлетворять ур-нию Янга - Бакстера, и с её помощью вводятся описанные выше ма-тем. конструкции КМОЗ - матрица монодромии 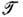и трансфер-матрица Т. Однако этих величин недостаточно для полного решения задачи. Особую проблему составляет учёт периодических граничных условий. В рамках КМОЗ эта проблема нахождения импульсов сводится к диагонализации трансфер-матрицы Т на т. н. нерегулярной решётке.

Одномерная модель Хаббарда. Гамильтониан одномерной цепочки Хаббарда (см. Зонный магнетизм )записывается в виде

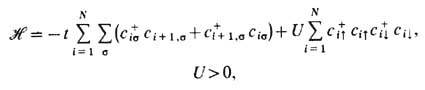
где 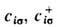-операторы уничтожения и рождения электрона на узле i со спином 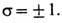Точное решение одномерной Хаббарда модели было дано в 1968 Э. Либом и Ф. By [5]. Решению этой задачи предшествовало точное решение Ян-том проблемы одномерной системы мн. частиц с d-образ-ным отталкиванием. В результате оказалось, что для полузаполненной зоны (т. е. в случае, когда число электронов, приходящихся на один узел, равно единице) осн. состояние одномерной модели Хаббарда для любого ненулевого значения кулоновского отталкивания U является диэлектрическим с антиферромагн. взаимодействием, но без дальнего порядка. В случае, когда зона заполнена не наполовину, Либ и By нашли, что эта система при U>0 должна быть проводящей.

Характерной чертой одномерной модели Хаббарда является разделение спиновой и зарядовой степеней свободы. В соответствии с этим в этой модели существуют два типа элементарных возбуждений. Со спиновой степенью свободы ассоциируется возбуждение фермиевской природы, имеющее спин ¹/₂ - спинон, а с зарядовой - х о л о н- элементарное возбуждение тоже фермиевской природы, несущее заряд, но не имеющее спина.

Использование квантового метода обратной задачи в одномерной модели Хаббарда позволяет продвинуться в решении более сложной задачи-определения асимптотики корреляц. ф-ций на больших расстояниях и вычисления соответствующих критич. показателей. Корреляц. ф-ции системы, находящейся в точке фазового перехода, т. е. при темп-ре абс. нуля для одномерной модели Хаббарда, могут быть найдены с помощью методов конформной теории поля.

Эффект Кондо. Ещё одним ярким достижением использования КМОЗ в статистич. механике явилось точное решение задачи о примесном атоме с локализов. магн. моментом, помещённом в немагн. кристалл. Первые исследования задачи о рассеянии электронов проводимости на такой примеси в следующих за борновским приближениях показали существенные температурные аномалии, в частности спиновую экранировку примеси при низких темп-pax. Совокупность этих явлений получила назв. Кондо эффекта. Долгое время эта проблема была предметом исследования, но все подходы к ней основывались на разл. вариантах теории возмущений. Точное решение этой задачи дано в 1980 П. Б. Вигманом [6] и Н. Андреем [7] независимо друг от друга. Были вычислены энергия осн. состояния и выражение для свободной энергии, позволившее получить такие термодинамич. величины, как примесная теплоёмкость и восприимчивость, представляющие в этой проблеме осн. интерес.

Модель Тирринга. Большие возможности для дальнейшего описания XYZ -модели даёт переход от дискретной цепочки к непрерывной струне, когда параметр цепочки 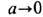. В этом пределе задача сводится к точно решаемой одномерной массивной модели Тирринга, хорошо известной в КТП. Эта модель описывает систему бесспиновых фермионов двух сортов, движущихся в противоположных направлениях со скоростью u:

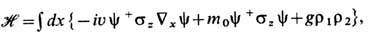
где 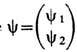-двухкомпонентный спинор, а r₁=(1/a)y₁⁺y₁

и r₂=(1/a)y₂⁺y₂ -плотности ферми-частиц сорта 1 и 2. Параметры модели Тирринга (u- скорость, т₀ - масса фермиона, g- константа связи между фермионами) находятся в след. соответствии с параметрами XYZ-модели:

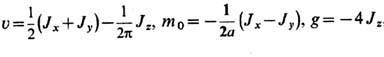
т. е. анизотропия в ( х, y )-плоскости соответствует массе фермиона, а параметр продольного обмена - межферми-онному взаимодействию.

Фермионная модель для безмассовых частиц ( т₀ = 0, J_x = J_y )наз. м о д е л ь ю Л а т т и н ж е р а. Она, очевидно, соответствует XXZ-модели в континуальном пределе. Точное решение этой модели может быть получено разными методами. Среди них вызывает интерес метод, основанный на идее б о з о н и з а ц и и ферми-систем. Оказывается, что модель Латтинжера, а также ряд др. моделей (среди них, напр., уже упоминавшаяся выше модель Хаббарда) демонстрируют совершенно необычное поведение с точки зрения теории обычной ферми-жидкости (системы взаимодействующих фермионов; см. Квантовая жидкость). Прежде всего это разделение спиновой и зарядовой степеней свободы и существование двух типов элементарных возбуждений фермиевской природы-нейтральных спинонов и заряж. холонов, а также существование необычных показателей корреляц. ф-ций. В отличие от ферми-жидкости, ф-ция распределения частиц по импульсам в осн. состоянии не имеет скачка на поверхности Ферми. Все эти свойства выделяют системы, к-рые точно решаются методом бозонизации, в особый класс взаимодействующих систем, получивший назв. ж и д к о с т и Л а т т и н ж е р а (см. [8]). Возможно, что эти необычные свойства при нек-рых условиях, в принципе, могут реализоваться и в системах с большой размерностью, что, естественно, позволит описать те эксперим. результаты, к-рые не вписываются в теорию обычной ферми-жидкости (напр., данные по высокотемпературной сверхпроводимости).

Завершая обсуждение XYZ -модели и всех моделей, сводящихся к ней, необходимо заметить, что все они эквивалентны квантовому синус-Гордона уравнению, прототипом к-poro является классич. одномерное нелинейное ур-ние. Создание квантового метода обратной задачи стимулировало поиск новых точных решений (см. [10-14]), причём они получены не только для одномерных квантовых систем, но также и для двумерной классич. гейзенберговской модели, где была использована инвариантность относительно конформных преобразований (А. М. Поляков и Вигман [9 ]).

Лит.:1) Bethe H., Theorie der Metalle. I. Eigenwerte und Eigen-funktionen der linearen Atom-Kette, "Z. Physik", 1931, Bd 71, S. 205; 2) Baxter R., One-dimensional anisotropic Heisenberg chain, "Ann. Phys.", 1972, v. 70, p. 323; 3) Taxтаджян А. Л., Фаддеев Л. Д., Квантовый метод обратной задачи и XYZ -модель Гёйзенберга, "Успехи матем. наук", 1979, т. 34, № 5, с. 13; 4) Yang С. N., Some exact results for many-body problem in one dimension with repulsive delta-function interaction, "Phys. Rev. Lett.", 1967, v. 19, p. 1312; 5) Lieb E. H., Wu F.Y., Absence of Mott transition in an exact solution of short-range 1-band model in 1 dimension, "Phys. Rev. Lett.", 1968, v. 20, p. 1445; 6) Вигман П. Б., Точное решение s - d обменной модели при T=0, "Письма в ЖЭТФ", 1980, т. 31, с. 392; 7) Andrei N., Diagonalization of the Kondo - Hamiltonian, "Phys. Rev. Lett.", 1980, v. 45, p. 379; 8) Haldane F. D. M., Luttinger liquid theory of one-dimensional quantum fluids. 1. Properties of the Luttinger model and their extension to the general 1 D interacting spinless Fermi gas, "J. Phys. C", 1981, v. 14, p. 2585; 9) Polyakov A. M., Wiegmann P. В., Theory of non-abelian Goldstone bosons in 2 dimensions, "Phys. Lett. B", 1983, v. 131, p. 121; 10) Бэкстер Р., Точно решаемые модели в статистической механике, пер. с англ., М., 1985; 11) Tsvelick A. M., Wiegmann Р. В., Exact results in the theory of magnetic alloys, "Adv. Phys.", 1983, v. 32, p. 453; 12) Годен M., Волновая функция Бете, пер. с франц., М., 1987; 13) Изюмов Ю. А., Скрябин Ю. Н., Статистическая механика магнитоупоря-доченных систем, М., 1987; 14) Боголюбов Н. М., Изергин А. Г., Корепин В. Е., Корреляционные функции интегрируемых систем и квантовый метод обратной задачи, М., 1992.

Ю. Н. Скрябин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.