СТРАННЫЙ АТТРАКТОР

СТРАННЫЙ АТТРАКТОР

- притягивающее множество неустойчивых траекторийв фазовом пространстве диссипативной динамической системы. С. а.,в отличие от аттрактора, не является многообразием (т. е. не является кривойили поверхностью); его геом. устройство очень сложно, а его структура фрактальна(см. Фракталы). Поэтому он получил назв. «странный» [Д. Рюэль (D.Ruelle), Ф. Такенс (F. Takens)]. Тот факт, что все траектории, расположенныев окрестности С. а., притягиваются к нему при , принципиально связан с характером неустойчивостей составляющих его траекторий, <к-рые неустойчивы по одним и устойчивы (притягивающи) по др. направлениям(т. е. являются седловыми; см. также Бифуркация, Предельный цикл). ТраекторииС. а. описывают стационарные стохастич. автоколебания, поддерживаемыев диссипативной системе за счёт энергии внеш. источника. С. а. характернылишь для автоколебат. систем, размерность фазового пространства к-рых большедвух (рис. 1). Первая исследовавшаяся система со С. а.- Лоренца система- трёхмерна.

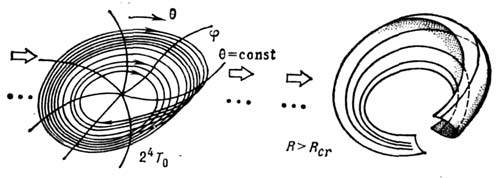
Рис. 1. Странный аттрактор в системе, описываемой уравнениями типа(1).

Системы с периодич. автоколебаниями, матем. образом к-рых является предельныйцикл, удаётся исследовать достаточно полно с помощью методов качественнойтеории дифференц. ур-ний. Построение же теории стохастических колебаний, заключающееся, в частности, в определении (предсказании) характеристики свойств С. а. по заданным параметрам системы, чрезвычайно затруднительнодаже для трёхмерных систем. Подобное построение удаётся провести, однако, <в тех случаях, когда в системе существует малый параметр, позволяющий спомощью отображения Пуанкаре перейти от анализа траекторий в трёхмерномпространстве к исследованию траекторий отображения.

Пример [1]. Подобно тому, как генератор Ван-дер-Поля является простейшими канонич. примером системы, демонстрирующей периодич. автоколебания, схема, <представленная на рис. 2а и определяющая несколько усложнённый генераторВан-дер-Поля, может служить одним из простейших примеров генераторов стохастич. <автоколебаний. От генератора Ван-дер-Поля с контуром в цепи сетки эта схемаотличается лишь включённым в контур последовательно с индуктивностью туннельнымдиодом или др. нелинейным элементом с вольт-амперной характеристикой, представленнойна рис. 2 б. Пока ток I в контуре и напряжение на сетке . малы, туннельный диод не оказывает существ. влияния на колебания вконтуре, и они, как и в обычном ламповом генераторе, нарастают. При этомчерез туннельный диод течёт ток I, а напряжение на нём определяетсяветвью характеристики I(V). Когда же ток I достигает значения I _т, происходит почти мгновенное переключение туннельного диода (быстротапереключения связана с малостью ёмкости С ₁) - скачкомустанавливается напряжение V_m. Затем ток через туннельныйдиод уменьшается и происходит его обратное переключение с участк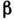а на 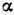. Врезультате двух переключений туннельный диод почти полностью поглощаетпоступившую в контур энергию и колебания начинают снова нарастать. (Прирассмотрении работы схемы характеристику лампы можно считать линейной;это оправдано тем, что в интересующем нас режиме колебания ограничиваютсянелинейной характеристикой туннельного диода.) Т. о., генерируемый сигнал U(t )представляет собой последовательность цугов нарастающих колебаний;окончание каждого цуга характеризуется скачком напряжения V(t).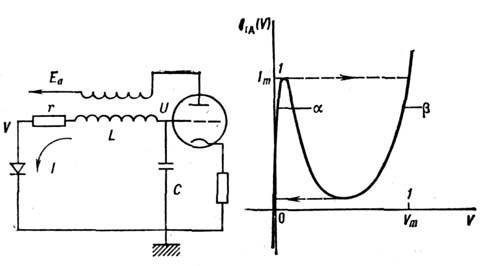

Рис. 2. Принципиальная схема (а) простого генератора шума- генератораВан-дер-Поля, в сеточный контур которого добавлен туннельный диод. Вольт-ампернаяхарактеристика (б) нелинейного элемента - туннельного диода.

Для количественного описания работы схемы исходные ур-ния

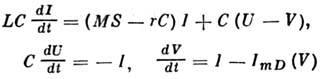
преобразуют к безразмерному виду:

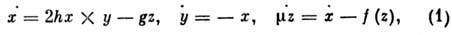
где x = I/I_m, z= V/V_m,

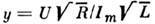
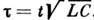
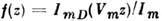- нормированнаяхарактеристика диода. Здесь 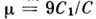- малый параметр 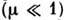Поэтому все движения в фазовом пространстве (рис. 3)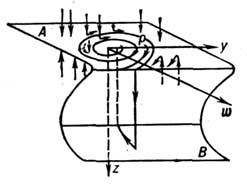

Рис. 3. Поведение траекторий в фазовом пространстве системы (1) при

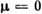
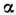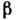можно разбить на быстрые переключения диода (прямые х =const, у =const) и медленные, при к-рых напряжение на диоде «следит» затоком; соответствующие траектории лежат на поверхностях А и В[х = f(z), f'(z) >0], отвечающих участкам и характеристикиДиода.

Система имеет одно неустойчивое [при 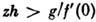] состояние равновесия х = у = z= 0 типа седло. Траектории, лежащиена поверхности А, раскручиваются вокруг неустойчивого фокуса и вконце концов достигают края поверхности А. Здесь происходит срывточки, отображающей на фазовой траектории состояние системы (т. н. изображающейточки) по линии быстрых движений на поверхность В. Пройдя по В, изображающая точка срывается обратно на поверхность А и попадаетв окрестность состояния равновесия - начинается новый цуг нарастающих колебаний. <Построенная картина движения соответствует реализации, представленной нарис. 4, и её спектру мощности.

Отображение Пуанкаре, соответствующее ур-ниям (1), при 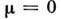кусочно можно описать непрерывной ф-цией, график к-рой приведён на рис.5. Линейный участок I с коэф. угла наклона, большим единицы, описываетраскручивание траектории на поверхности медленных движений А, соответствующейнарастанию колебаний в контуре. Участок II описывает этап возвращения траекторий, <сорвавшихся с поверхности А на поверхность В, обратно на А (см. рис. 3). Все траектории, лежащие вне основания обозначенногопунктиром квадрата, входят в него при асимптотически больших значенияхвремени, т. е. область D- поглощающая и содержит аттрактор. Всетраектории внутри этой области неустойчивы, т. е. аттрактор является странным. <При малых значениях 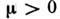свойства стохастичности движений (как показывают численные исследования)сохраняются.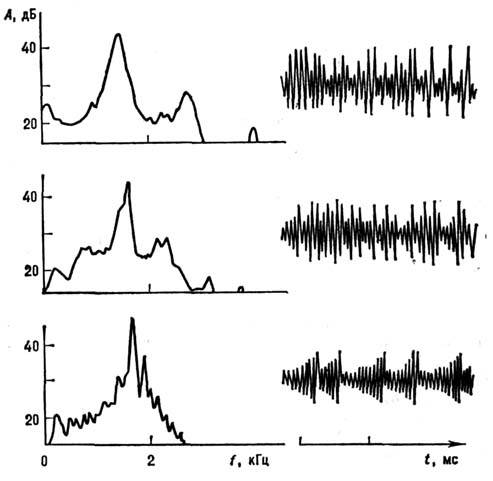

Рис. 4. Спектр мощности сигнала, генерируемого схемой, представленнойна рис. 2а, и осциллограмма этого сигнала.

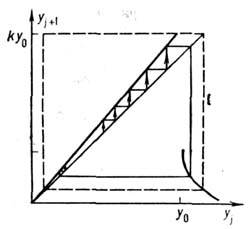
Рис. 5. График функции f(x), описывающей динамику схемы рис. 2 при .

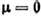Фрактальная размерность. Все разнообразие статистич. свойств случайногосигнала, порождаемого динамич. системой со С. а., может быть описано, еслиизвестно распределение вероятности состояний системы. Однако получить (ииспользовать) это распределение для конкретных систем со С. а., чрезвычайносложно (хотя бы потому, что плотность распределения инвариантной вероятностноймеры всегда сингулярна). Это одна из причин, по к-рой для описания С. а. <и сопоставления его свойств со свойствами реального сигнала используютразл. рода усреднённые характеристики. Наиб. широко используемыми являютсявсевозможные размерностные характеристики, в частности фрактальная размерность(см. также [2-4])

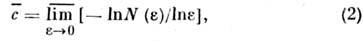
где , нек-рый фиксированный параметр,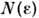- число n -мерных шаров диаметра 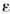,покрывающих С. а. динамич. системы с n -мерным фазовым пространством.

Определённая согласно ур-нию (2) размерность с не может, очевидно, <превышать n, но может быть меньше п(n -мерные шарымогут оказаться почти пустыми). Для «обычных» множеств ур-ние (2) даёточевидные результаты. Так, для множества из k точек 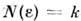,; дляотрезка длины L прямой лилии ,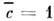;для куска площади S двумерной поверхности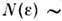 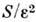,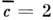и т. д. Неравенство размерности целому числу соответствует сложному геом. <устройству. Для генератора, изображённого на рис. 1, размерность соответствующегоаттрактора системы (1) в широком диапазоне изменения параметров остаётсязаключённой в интервале (2,3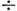2,6).

С физ. точки зрения, осн. «достоинство» фрактальной размерности С. а. <в том, что она даёт оценку эфф. числа степеней свободы, формирующих установившийся(после окончания всех переходных процессов) стохастич. сигнал. Более строгоесоотношение между размерностью 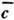и числом степеней свободы га имеет вид:

Бифуркации странных аттракторов. Пути рождения стохастич. <автоколебаний при изменении управляющего параметра (напр., коэф. усиленияв генераторе рис. 1) зависят от конкретных свойств исследуемой системы. <Однако как и предельный цикл, к-рый может родиться лишь несколькими типичнымиспособами, так и С. а. обладают сравнительно небольшим числом наиб. типичныхвозможностей возникновения [1,4-6].

Сценарий Фейгенбаума - цепочка бифуркаций удвоения периода устойчивогопредельного цикла. Если при изменении управляющего параметра периодич. <движение теряет устойчивость, то вместо него может возникнуть др. устойчивоедвижение (напр., квазипериодическое, лежащее на притягивающем двумерномторе) либо предельный цикл удвоенного периода; последнему случаю соответствуетпереход мультипликатора через (-1). В n -мерном фазовом пространствеповедение траекторий отображения Пуанкаре в окрестности претерпевающегобифуркацию удвоения периода предельного цикла определяется ф-цией, напр.,f(x), график к-рой похож на параболу. Эта ф-ция описывает связьмежду координатами в направлении собств. подпространства оператора линеаризацииотображения Пуанкаре, отвечающего мультипликатору (-1) (j + 1)-гои j-го пересечений траекторией системы секущей Пуанкаре: x_j+1= f(x_j). Возникшему устойчивому предельному циклуудвоенного периода отвечает двупериодич. траектория отображения f.При дальнейшем изменении параметра бифуркации удвоения периода бесконечноповторяются, а бифуркац. значения, напр.,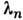накапливаются к критич. точке 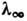, отвечающей возникновению С. а. В соответствии со сценарием Фейгенбаумаимеет место универсальный (не зависящий от конкретной системы) закон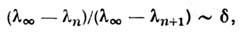

где 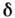= 4,6692... - универсальная константа Фейгенбаума (см. Фейгенбаума универсальность).

Родившемуся С. а. при фиксированном 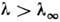отвечает неск. интервалов на оси х; участки между этими интерваламисодержат притягивающиеся к аттрактору траектории, а также 2^m -периодические(относительно отображения f), неустойчивые предельные циклы, начинаяс нек-рого m₀ и меньше. При увеличении параметра 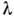скорость разбегания траекторий на С. а. увеличивается, и он «разбухает»,последовательно поглощая неустойчивые предельные циклы периодов 2 ^т+1,2 ^т, ... При этом число отрезков, отвечающих аттрактору, <уменьшается, а их длины увеличиваются. Возникает как бы обратный каскадпоследоват. упрощений аттрактора. Рис. 6 иллюстрирует этот процесс длядвух последних бифуркаций. На рис. 6а «лента» аттрактора совершает 4 оборота, <после бифуркации она становится двухоборотной и затем, после следующейбифуркации, замыкается на себя всего через один оборот, предварительноперекрутившись (6б и 6в).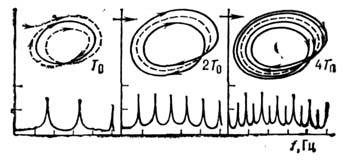

Рис. 6. «Обратные бифуркации» удвоения периода, иллюстрирующие разбуханиеаттрактора, возникшего по сценарию Фейгенбаума.

Перемежаемость. Во мн. системах при прохождении управляющего параметра(скажем, 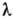)через бифуркац. значение 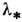переход к стохастич. автоколебаниям внешне осуществляется как редкое нарушениерегулярных колебаний «стохастич. всплесками». При этом длительность ламинарной(регулярной) фазы тем больше, чем меньше надкритичность 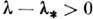С ростом же надкритичности длительность регулярной фазы сокращается. Этакартина интерпретируется следующей эволюцией осн. объектов в фазовом пространстве, <определяющих бифуркации (предельные циклы, сепаратрисы седловых периодич. <траекторий и пр.). В момент бифуркации сливаются и исчезают отвечающийавтоколебаниям устойчивый предельный цикл и седловая периодич. траектория. <При малой надкритичности все траектории, стремившиеся ранее к устойчивомупредельному циклу, долгое время сохраняют характер своего поведения, т. <е. демонстрируют движение, близкое к периодическому. С течением времени 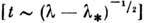они «замечают», что старый аттрактор исчез, и, оставаясь рядом с сепаратрисой(также исчезнувшей) седлового предельного цикла, уходят в др. часть фазовогопространства. Если в докритич. области система была глобально устойчива(т. е. существовал только один притягивающий объект), то эти траекториичерез нек-рое время вновь попадают в окрестность исчезнувшего предельногоцикла. Если при этом в докритич. области значений параметров сепаратрисаседлового цикла была вложена в фазовое пространство достаточно сложнымгеом. образом (образовывала бесконечное число складок - «гофрировалась»,содержала гетероклинич. траектории др. седловых циклов и т. п.), то естьпереходный процесс демонстрировал нерегулярное поведение, то время попаданияв окрестность исчезнувшего цикла уже будет являться случайной величиной. Далее повторяется ламинарная фаза, <предшествующая новому, «турбулентному», всплеску и т. д.

Кроме этих основных способов возникновения С. а. достаточно часто встречаютсятакже переходы к хаотич. автоколебаниям через разрушение квазипериодических(в фазовом пространстве при изменении управляющих параметров теряет гладкостьи разрушается притягивающий двумерный тор) и комбинированные сценарии [6].

Многомерные странные аттракторы часто обнаруживаются всистемах с большим числом степеней свободы. Среди возможных механизмов, <объясняющих существование многомерных С. а., выделяются следующие: 1) вмногомерном фазовом пространстве в докритич. ситуации существуют непритягивающеестохастич. множество и маломерный С. а. В момент бифуркации маломерныйаттрактор перестаёт быть таковым, а бывшее непритягивающим стохастич. множествовысокой размерности вливается в возникший жёстким образом (скачком) многомерныйаттрактор; 2) при изменении параметров в аттракторе происходит постепеннаянепрерывная перестройка его структуры, при к-рой размерность аттракторамонотонно увеличивается. Здесь можно выделить два случая: а) при изменениипараметра в аттракторе рождаются седловые траектории со всё большим числомнеустойчивых направлений; б) число неустойчивых направлений сохраняется, <но возрастает скорость разбегания траекторий вдоль этих направлений. Стохастич. <автоколебания распределённых систем (с бесконечномерным фазовым пространством)имеют много общего с движением динамических диссипативных систем, описываемыхсистемами конечного числа обыкновенных дифференц. ур-ний. Связь эта объясняетсядействием высокочастотной диссипации (в гидродинамике, напр., это - вязкость).Такая диссипация лишает мелкомасштабные возбуждения среды самостоятельности, <в результате чего описывающие их движение ф-ции начинают алгебраическизависеть от соответствующих ф-ций, отвечающих крупномасштабным возбуждениям. <Т. о., реально движение бесконечномерной системы описывается траекториями, <лежащими на конечномерном (хотя, возможно, высокой размерности) С. а. Неупорядоченноетечение в области перехода к турбулентности также представляет собой движениена С. а. (см. Турбулентность).

Лит.:1) Рабинович М. И., Трубецков Д. И., Введение в теориюколебаний и волн, М., 1984; 2) Лихтенберг А., Либерман М., Регулярная истохастическая динамика, пер. с англ., М., 1984; 3) Афраймович В. С., РейманА. М., Размерность и энтропия в многомерных системах, в кн.: Нелинейныеволны. Динамика и эволюция, под ред. А. В. Гапонова-Грехова, М. И. Рабиновича, <М., 1989; 4) Шустер Г., Детерминированный хаос. Введение, пер. с англ.,М., 1988; 5) Ландау Л. Д., Лифшиц Е. М., Гидродинамика, 4 изд., М., 1988;6) Афраймович В. С., Внутренние бифуркации и кризисы аттракторов, в кн.:Нелинейные волны. Структуры и бифуркации, под ред. А. В. Гапонова-Грехова, <М. И. Рабиновича, М., 1987; 7) Гидродинамические неустойчивости и переходк турбулентности, под ред. X. Суинни, Дж. Голлаба, пер. с англ., М., 1984;8) Рабинович М. И., Сущик М. М., Регулярная и хаотическая динамика структурв течениях жидкости, «УФН», 1990, т. 160, с. 3. В. С. Афраймович, М. <И. Рабинович.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.