СТАТИСТИЧЕСКИЙ КРИТЕРИЙ

СТАТИСТИЧЕСКИЙ КРИТЕРИЙ

- определяющие правила, согласно к-рымпо результатам наблюдений принимается решение в задаче статистическойпроверки гипотез. С. к. строится следующим образом. Выбирается проверочнаястатистика - ф-ция данных наблюдений х и проверяемой гипотезы Пространство всех возможных значений X разбивается на две области - критическуюw и допустимую . Если реализовавшееся в эксперименте значение проверочной статистики . попадает в критич. область со, то гипотеза Н ₀ отвергается, <в противном случае гипотеза Н ₀ считается непротиворечащейрезультатам эксперимента и принимается. Размер критич. области со выбираетсятаким, чтобы вероятность отвергнуть гипотезу, когда она верна, т. е. величина , была бы малой. Величину 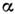наз. уровнем значимости данного критерия или ошибкой 1-го рода.

В тех случаях, когда есть только одна гипотеза Н ₀, т. <е. стоит задача подтверждения или опровержения Н ₀, используемыекритерии наз. критериями согласия. Для данных, сгруппированных в гистограмму, наиб. популярными являются следующие два критерия.- критерий Пирсона. Как известно, ф-ция плотности вероятности мультиноминального распределения, к-рому подчиняются числа событий в бинах (каналах)гистограммы, в асимптотике по числу событий сходится к ф-ции плотностивероятности нормального распределения. Это позволяет показать, что статистика

где n_i- число событий в i-м бине гистограммы, .- число бинов, N - полное число событий, p_i - вероятность попадания события в i-й бин, согласно гипотезе Н ₀, распределена по -распределению с k -1 степенями свободы. Выбирая (1) в качестве проверочной статистикии критич. область , получаем 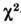критерий Пирсона с уровнем значимости

Критерий серий использует информацию о знаках разностей n_i- Np_i, к-рая теряется в -критерии. <Если гипотеза H₀ полностью определена (простая гипотеза),то критерий серий не зависит от 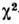критерия для той же самой гистограммы и несёт независимую дополнит. информацию. <Назовём серией последовательность отклонений п _i - Np_i одного знака. Если гипотеза Н ₀ верна, то оба видазнаков отклонений равновероятны. Это позволяет вычислить распределениевероятности для числа серий R. Выбирая в качестве проверочной статистикивеличину R и в качестве критич. област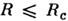и при ,получим критерий серий с уровнем значимости .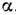

Более эфф. критериями проверки гипотезы H₀ являютсякритерии, предложенные Н. В. Смирновым и А. Н. Колмогоровым. Они используютв качестве проверочных статистик разл. «расстояния» между экспериментальной(выборочной) ф-цией распределения

и ф-цией распределения F₀(x), отвечающей гипотезе Н ₀. Критерий Смирнова - Крамера - М и з е с а в качествепроверочной статистики использует ф-цию где f(x)- плотность ф-ции распределения F₀(x). Н. <В. Смирновым вычислена плотность распределения вероятности величины NW² в асимптотич. пределе Критерий Колмогорова использует в качестве проверочной статистики ф-цию

асимптотич. распределение к-рой было получено Колмогоровым. Численныезначения ф-ций распределения NW* и можно найти в [1]. Др. критерии проверки гипотезы H₀ можно найти в [1-3].

Пусть теперь кроме гипотезы Н ₀ есть альтернативнаяпростая гипотеза Н ₁ и стоит задача выбора одной из нихна основании вектора измерений х. В этом случае вводится величина, <называемая мощностью критерия, к-рая определяется как вероятность 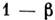попадания X в критич. область со, когда верна гипотеза H₁, т. е.. Мощность прямо связана с вероятностью принятия ложной гипотезы (ошибка2-го рода):.Мощность позволяет сравнивать критерии между собой: наилучшим критериемдля сравнения H₀ и Н ₁ с данным уровнемзначимости а служит критерий с макс, мощностью. Задачу поиска наиб. мощногокритерия можно свести к задаче нахождения наилучшей критич. области в Х-пространстве. <Решением последней задачи является критерий Неймана - Пирсона: если 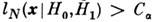, то принимается Н ₁; если , то принимается Н ₀. Здесь 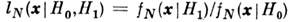- отношение правдоподобия,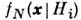- ф-ция плотности вероятности х, если справедлива гипотеза H_i,а выбранотаким образом, чтобы выполнялось условие

Область со состоит из тех точек пространства , в к-рых 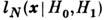принимает наиб. значения. Критерий наз. состоятельным, если
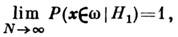т. е. <если критерий с ростом числа наблюдений всё лучше разделяет гипотезы. Критерийназ. несмещённым, если для любой альтернативной гипотезы Н ₁ критич. область выбрана так, что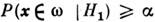

Если гипотеза H₀ или Н ₁ (или обе)не являются полностью определёнными (сложные гипотезы), то не существуетоптим. метода конструирования наилучшего критерия. На практике в качествепроверочной статистики обычно используется отношение максимумов правдоподобия[2].

Лит.:1) Большев Л. Н., Смирнов Н. В., Таблицы математическойстатистики, 3 изд., М., 1983; 2) Статистические методы в экспериментальнойфизике, пер. с англ., М., 1976; 3) К е н д а л л М., С т ь ю а р т А.,Статистические выводы и связи, пер. с англ., М., 1973. В. П. Жигунов, <С. В. Клименко.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.