- НЕУСТОЙЧИВОСТЬ В КОЛЕБАТЕЛЬНЫХ И ВОЛНОВЫХ СИСТЕМАХ
- НЕУСТОЙЧИВОСТЬ В КОЛЕБАТЕЛЬНЫХ И ВОЛНОВЫХ СИСТЕМАХ
-
- самопроизвольное нарастание возмущений на фоне заданного движения, приводящее к качественному изменению поведения системы. Простейший пример неустойчивого состояния - равновесие маятника в верх. точке (рис. 1). Любое сколь угодно малое возмущение маятника приводит к его уходу от состояния равновесия. Физически неустойчивость движения системы означает, что состояние равновесия может быть реализовано лишь приближённо и на огранич. интервале времени (для волновых систем - и пространства), тем меньшем, чем выше скорость нарастания возмущений. Состояния или движения системы, малые нач. возмущения к-рых остаются малыми и в дальнейшем, наз. устойчивыми. Примерами являются соответственно состояние равновесия маятника в ниж. точке и само колебат. движение маятника.
Понятия неустойчивости и устойчивостидвижения относятся ко всем динамическим системам, а не только кколебательным и волновым.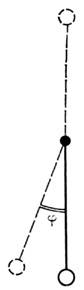
Рис. 1. Маятник с жёстким подвесом.
Строгая формулировка понятия устойчивости, <пригодная для любых систем, затруднительна, поэтому, как правило, учитываетсяспецифика задачи. Так, различают устойчивость движения в "малом" - по отношениюк бесконечно малым возмущениям и в "большом" - по отношению к возмущениямконечной величины, устойчивость по отношению к определ. классу возмущенийи т. д. Наиб. изучена устойчивость в "малом", т. к. при малых возмущенияхвозможно разложение по ним в окрестности исследуемого движения исходныхур-ний, описывающих систему (см. Устойчивость движения, Устойчивостьравновесия). Специфика колебательных и волновых систем заключаетсялишь в характере движений в системе и в характере нарастающих при неустойчивостивозмущений, а также в физ. механизмах Н. в к. и в. с. Одной из осн. стадийизучения поведения колебательных и волновых систем является отыскание простыххарактерных состояний и движений: состояний равновесия и периодич. режимовв колебательных системах или стационарных и автомодельных режимов в волновыхсистемах. Затем исследуется их устойчивость как условие реализуемости. <В случае неустойчивости движения анализируются характер нарастающих возмущений, <закон и скорость их нарастания, а также механизм неустойчивости. Традиционноразделяют неустойчивость "тривиальных" состояний системы (состояний равновесияи пространственно однородных стационарных режимов) и неустойчивость колебанийи волн. В первом случае речь идёт о зарождении колебательных и волновыхдвижений из состояния покоя, а во втором - о разрушении существующих всистеме колебательных и волновых процессов. Нарастание возмущений на фоненеустойчивого движения может происходить в виде колебании или волн либоапериодически. Поступление энергии к нарастающим периодическим возмущениямпри Н. в к. и в. с. может идти двумя способами - автоколебательным и резонансным(см. Автоколебания). При автоколебательной неустойчивости возмущениярастут за счёт энергии источников неколебательной природы. Резонансноенарастание возмущений обусловлено отбором ими энергии от к.-л. периодическихисточников или движений системы. Основные особенности Н. в к. и в. с. могутбыть продемонстрированы на примере матем. маятника. Движение его в отсутствиедиссипации описывается ур-нием
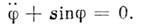
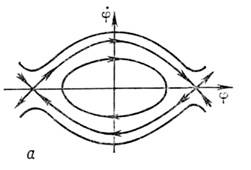
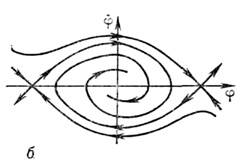
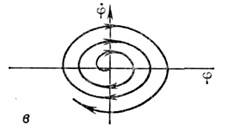
Рис. 2. Фазовые портреты: а - математическогомаятника; б - математического маятника с диссипацией; в - неустойчивогосостояния равновесия.
Замкнутые траектории на рис. 2, . отвечаютпериодич. незатухающим колебаниям. При введении в систему малой диссипациии соответственно в ур-ние осциллятора члена
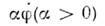 колебания станут затухающими и замкнутые траектории на фазовой плоскостипревратятся в скручивающиеся спирали (рис. 2, б). Если возможнопоступление энергии к колебаниям, то они будут нарастать. Подталкивая маятникс периодом его собств. колебаний, можно получить резонансное возбуждениеколебаний. Представим теперь, что воздействие на маятник зависит от характераего колебаний благодаря механизму обратной связи, обеспечивающемупоступление энергии в нужной фазе, пропорциональное, напр., величине
колебания станут затухающими и замкнутые траектории на фазовой плоскостипревратятся в скручивающиеся спирали (рис. 2, б). Если возможнопоступление энергии к колебаниям, то они будут нарастать. Подталкивая маятникс периодом его собств. колебаний, можно получить резонансное возбуждениеколебаний. Представим теперь, что воздействие на маятник зависит от характераего колебаний благодаря механизму обратной связи, обеспечивающемупоступление энергии в нужной фазе, пропорциональное, напр., величине 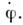 Формально это соответствует введению в систему отрицат. диссипации
Формально это соответствует введению в систему отрицат. диссипации 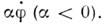 Тогда состояние равновесия
Тогда состояние равновесия 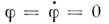 существует, но оно неустойчиво - сколь угодно малое отклонение от указаннойточки приведёт к раскачке колебаний. Фазовые траектории в окрестности состоянияравновесия имеют при этом вид раскручивающихся спиралей (рис. 2, в). Т. <к. частота и фаза поступления энергии к колебаниям определяются собств. <движением осциллятора, то источник энергии может быть неколебательным. <Это пример автоколебат. неустойчивости. Автоколебат. неустойчивость, ограниченнаянелинейными эффектами, приводит, как правило, к установлению стационарныхавтоколебаний. В более сложных системах с размерностью фазового пространства, <не меньшей трёх, неустойчивость может привести к возникновению стохастическихколебаний. Наряду с механизмом положит. обратной связи к автоколебат. <неустойчивости приводит существование падающего участка на характеристикезависимости силы трения в осцилляторе от скорости движения. Так происходит, <напр., возбуждение струны движущимся смычком. Зависимость силы трения ототносит. скорости движения смычка и струны показана на рис. 3. Выбраннойскорости движения смычка v0 отвечает сила F0, к-раяуравновешивается натяжением струны. Легко, однако, заметить, что указанноесостояние равновесия неустойчиво. Появление скорости движения струны, напр.,в направлении движения смычка означает уменьшение относит. скорости смычкаи струны и соответственно вызывает возрастание силы трения F. Этоведёт к уходу от состояния равновесия. В результате возникают нарастающиеколебания струны, что следует и из энергетич. баланса. Действительно, работасилы трения за период движения струны положительна: в те полпериода, чтоструна движется со смычком, сила трения больше, чем при встречном их движении. <С автоколебат. неустойчивостью связана работа генераторов периодич. колебаний(механич., акустич., эл.-магн. и т. д.). В частности, в механич. часахпотери на трение компенсируются при помощи анкерного механизма за счётэнергии пружины. Электрич. колебания генерируются в колебат. контуре засчёт энергии батареи либо при помощи триода с включением контура в цепьего управляющего электрода (обратная связь), либо при включении в контуртуннельного диода - элемента с падающим участком вольт-амперной характеристики.
существует, но оно неустойчиво - сколь угодно малое отклонение от указаннойточки приведёт к раскачке колебаний. Фазовые траектории в окрестности состоянияравновесия имеют при этом вид раскручивающихся спиралей (рис. 2, в). Т. <к. частота и фаза поступления энергии к колебаниям определяются собств. <движением осциллятора, то источник энергии может быть неколебательным. <Это пример автоколебат. неустойчивости. Автоколебат. неустойчивость, ограниченнаянелинейными эффектами, приводит, как правило, к установлению стационарныхавтоколебаний. В более сложных системах с размерностью фазового пространства, <не меньшей трёх, неустойчивость может привести к возникновению стохастическихколебаний. Наряду с механизмом положит. обратной связи к автоколебат. <неустойчивости приводит существование падающего участка на характеристикезависимости силы трения в осцилляторе от скорости движения. Так происходит, <напр., возбуждение струны движущимся смычком. Зависимость силы трения ототносит. скорости движения смычка и струны показана на рис. 3. Выбраннойскорости движения смычка v0 отвечает сила F0, к-раяуравновешивается натяжением струны. Легко, однако, заметить, что указанноесостояние равновесия неустойчиво. Появление скорости движения струны, напр.,в направлении движения смычка означает уменьшение относит. скорости смычкаи струны и соответственно вызывает возрастание силы трения F. Этоведёт к уходу от состояния равновесия. В результате возникают нарастающиеколебания струны, что следует и из энергетич. баланса. Действительно, работасилы трения за период движения струны положительна: в те полпериода, чтоструна движется со смычком, сила трения больше, чем при встречном их движении. <С автоколебат. неустойчивостью связана работа генераторов периодич. колебаний(механич., акустич., эл.-магн. и т. д.). В частности, в механич. часахпотери на трение компенсируются при помощи анкерного механизма за счётэнергии пружины. Электрич. колебания генерируются в колебат. контуре засчёт энергии батареи либо при помощи триода с включением контура в цепьего управляющего электрода (обратная связь), либо при включении в контуртуннельного диода - элемента с падающим участком вольт-амперной характеристики.Примером др. типа неустойчивости - резонансной- может служить параметрич. неустойчивость маятника. Если с частотой, вдвоебольшей частоты маятника, менять длину подвеса, то состояние равновесия
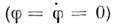 и в этом случае оказывается неустойчивым. Именно так возникает раскачкакачелей, если вставать при прохождении ниж. точки траектории (см. Параметрическийрезонанс, Параметрическая генерация и усиление электромагнитных колебаний).
и в этом случае оказывается неустойчивым. Именно так возникает раскачкакачелей, если вставать при прохождении ниж. точки траектории (см. Параметрическийрезонанс, Параметрическая генерация и усиление электромагнитных колебаний).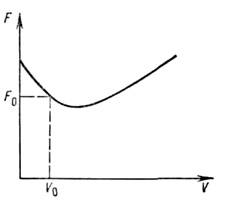
Рис. 3. Зависимость силы трения F междусмычком и струной от их относительной скорости.
Нарастание колебаний маятника при периодическомизменении длины его подвеса может быть рассмотрено и с др. точки зрения- как пример неустойчивости периодических колебаний. При замене жёсткогоподвеса маятника упругим система приобретает дополнит. степень свободы, <соответствующую вертикальным колебаниям. При произвольном соотношении частотвертикальные и горизонтальные колебания могут происходить практически независимо. <Напр., возможны незатухающие вертикальные колебания груза на пружине. Привыполнении условия параметрич. резонанса два типа колебаний начинают эффективновзаимодействовать, что в рассматриваемом случае приводит к раскачке горизонтальныхколебаний за счёт энергии вертикальных. При этом вертикальные колебанияв системе оказываются неустойчивыми по отношению к возбуждению горизонтальных.
Проявления неустойчивости в колебат. системахс конечным числом степеней свободы в осн. аналогичны рассмотренным на примеремаятника. Проявление неустойчивости в волновых системах имеет особенности, <обусловленные пространств. протяжённостью этих систем. Как и в колебат. <системах, неустойчивость волновых движений в консервативных волновых системахявляется резонансной и связана с нелинейным взаимодействием волн, напр. <трёх-, четырёх- и т. д. волновые взаимодействия, возникающие в нелинейныхсредах при выполнении условий синхронизма, самовоздействие волн (самомодуляция, <самофокусировка) и др. В активных волновых системах неустойчивость можетиметь как автоколебательный, так и резонансный характер. Примерами активныхволновых систем являются лазеры, гиротроны, волновые пучки в плазме, химическиактивные среды. При автоколебат. неустойчивости волновые возмущения нарастаютза счёт энергии неколебат. источников, напр. пучков частиц или течений. <В отличие от колебат. систем нарастание возмущений в таких системах можетпроисходить не только во времени, но и в пространстве. В частности, возмущениеможет носить характер бегущего волнового пакета нарастающей амплитуды иуходить из области своего зарождения. После прохода бегущего возмущениячерез элемент системы, от к-рого оно отбирает энергию, поле возмущенийв этой области может с течением времени стремиться к нулю. Это т. н. конвективная(сносовая) неустойчивость. Если же возмущения нарастают с течением времениво всех точках пространства, то неустойчивость является абсолютной. Системы, <в к-рых реализуется конвективная неустойчивость, служат основой для созданияусилителей, а системы с абс. неустойчивостью являются генераторами. Существуюткритерии определения характера неустойчивости в волновых системах. Однаково многих реальных системах разделение на абсолютную и конвективную неустойчивостьневозможно. В частности, либо замыкая отрезок конвективно неустойчивойсистемы в кольцевую систему, либо включая внеш. обратную связь, получаютсистему с абс. неустойчивостью (см. Автоволны, Волны, Нелинейные системы идр.).Лит.: Андронов А. А., Витт А. А.,Xайкин С. Э., Теория колебаний, 3 изд., М., 1981; Бутенин Н. В., НеймаркЮ. И., Фуфаев Н. А., Введение в теорию нелинейных колебаний, 2 изд., М.,1987; Федорченко А. М., Коцаренко Н. Я., Абсолютная и конвективная неустойчивостьв плазме и твердых телах, М., 1981; Рабинович М. И., Трубецков Д. И., Введениев теорию колебаний и волн, М., 1984.
А. Я. Васович, А. А. Новиков.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
