- ДИСПЕРСИОННОЕ УРАВНЕНИЕ
- ДИСПЕРСИОННОЕ УРАВНЕНИЕ
-
-соотношение, связывающее циклич. частоты
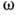 и волновые векторы k собственных гармонич. волн ( нормальных волн )в линейных однородных системах: непрерывных средах, волноводах, передающих линиях и др. Д. <у. записывается в явном
и волновые векторы k собственных гармонич. волн ( нормальных волн )в линейных однородных системах: непрерывных средах, волноводах, передающих линиях и др. Д. <у. записывается в явном 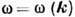 или неявном
или неявном 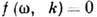 виде. В тех случаях, когда зависимость
виде. В тех случаях, когда зависимость 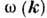 неоднозначна, выделяют однозначные ветви Д. <у.:
неоднозначна, выделяют однозначные ветви Д. <у.: 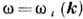 (где n= 1, 2, ...), соответствующие нормальным модам системы, т. е. совокупностям нормальных волн с одинаковой (в т. ч. поляризационной) структурой. Графич. изображение корней Д. у. на плоскости
(где n= 1, 2, ...), соответствующие нормальным модам системы, т. е. совокупностям нормальных волн с одинаковой (в т. ч. поляризационной) структурой. Графич. изображение корней Д. у. на плоскости 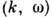 наз. дисперсионной кривой.
наз. дисперсионной кривой.
Д. у. эквивалентно полному кинематич. описанию волновых процессов в системе. В частности, Д. у. определяет фазовые скорости гармонич. волн в направлении k
 , групповые скорости перемещения квазигармонич. одномодовых волновых пакетов
, групповые скорости перемещения квазигармонич. одномодовых волновых пакетов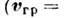
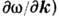 , расплывание пакетов (зависящее от величин вторых
, расплывание пакетов (зависящее от величин вторых 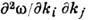 или более высоких производных). В области комплексных значений
или более высоких производных). В области комплексных значений 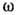 и
и 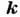 Д. у. определяет временные
Д. у. определяет временные 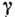 и пространственные Г инкременты (или декременты) процессов распространения волн
и пространственные Г инкременты (или декременты) процессов распространения волн 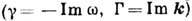 (см. Дисперсия волн).
(см. Дисперсия волн).
Д. у. являются следствием динамических (в общем случае интегродифференциальных) ур-ний движения и краевых условий на границах раздела сред. И наоборот, по виду Д. у. иногда (при наличии определённой априорной информации о системе) или во всех случаях, когда Д. у. представлено через полиномы по
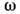 и k, могут быть восстановлены динамич. ур-ния процессов с помощью замены
и k, могут быть восстановлены динамич. ур-ния процессов с помощью замены
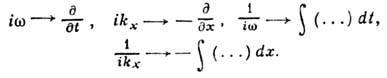
Д. у. позволяет установить общность между волновыми движениями разл. природы: так, напр., одно и то же соотношение
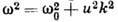 соответствует: 1) эл.-магн. волнам в изотропной плазме (при этом
соответствует: 1) эл.-магн. волнам в изотропной плазме (при этом 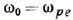 - плазменная частота, u=c- скорость света в вакууме); 2) плазменным волнам (
- плазменная частота, u=c- скорость света в вакууме); 2) плазменным волнам (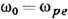 ,
, 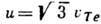 ,
, 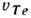 - тепловая скорость электронов); 3) волнам в радиоволноводах (u=c,
- тепловая скорость электронов); 3) волнам в радиоволноводах (u=c, 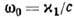 ,
, 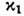 -поперечное волновое число, определяемое размерами, конфигурацией волновода, типом и номером моды); 4) волнам в волноводах акустических(u=cS- скорость звука.
-поперечное волновое число, определяемое размерами, конфигурацией волновода, типом и номером моды); 4) волнам в волноводах акустических(u=cS- скорость звука. 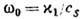 ); 5) элементарной частице в релятивистской волновой механике ( и = с,
); 5) элементарной частице в релятивистской волновой механике ( и = с,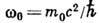 , m0 - масса покоя).
, m0 - масса покоя).
В плавно неоднородных средах, где гармонические во времени поля можно представить в виде
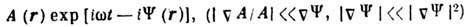 ,
,
обобщением Д. у. является уравнение эйконала
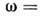
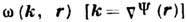 ., к-рое совпадает при фиксиров. значении координаты r с Д. у. в соответствующей однородной среде. Ур-нию эйконала можно сопоставить систему лучевых ур-ний (см. Геометрической оптики метод):
., к-рое совпадает при фиксиров. значении координаты r с Д. у. в соответствующей однородной среде. Ур-нию эйконала можно сопоставить систему лучевых ур-ний (см. Геометрической оптики метод): 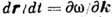 ,
, 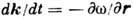 . Аналогичным образом Д. у. обобщается на системы с медленно меняющимися во времени параметрами (параметрические колебательные системы).
. Аналогичным образом Д. у. обобщается на системы с медленно меняющимися во времени параметрами (параметрические колебательные системы).
При исследовании нелинейных систем Д. у. позволяет описать волновые процессы вблизи стационарных состояний и установить их устойчивость или характер их неустойчивости. При этом Д. у. составляется для линеаризов. ур-ний, описывающих малые отклонения от стационарного состояния. По виду Д. у. можно определить тип неустойчивости: если действительным k соответствуют комплексные значения
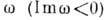 , то имеет место абсолютная неустойчивость системы, если действительным
, то имеет место абсолютная неустойчивость системы, если действительным 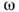 соответствуют комплексные значения
соответствуют комплексные значения 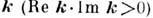 , неустойчивость является конвективной (см. Неустойчивость в колебательных и волновых системах).
, неустойчивость является конвективной (см. Неустойчивость в колебательных и волновых системах).
Существует обобщение Д. у. на существенно нелинейные стационарные волновые процессы (периодические нелинейные волны или уединённые волны - солитоны). В этом случае нелинейное Д. у. связывает амплитуду стационарной волны с её структурными параметрами - характерными временами и масштабами (см. Нелинейные колебания и волны).
При квантовом подходе Д. у. приобретает смысл соотношения между энергией
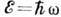 и импульсом
и импульсом 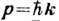 (см. Дисперсии закон).
(см. Дисперсии закон).
Лит.: Крауфорд Ф., Волны, пер. с англ., 3 изд., M., 1984; Уизем Дж., Линейные и нелинейные волны, пер. с англ., M., 1977. M. А. Миллер, Г. В. Пермитин.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
