КОНВЕКТЙВНАЯ НЕУСТОЙЧИВОСТЬ.

КОНВЕКТЙВНАЯ НЕУСТОЙЧИВОСТЬ.

1) К. н. (сно-совая неустойчивость) - тип неустойчивости в системе с распределёнными параметрами, при к-ром малое начальное возмущение нарастает во времени и сносится в пространстве (см. Абсолютная неустойчивость, Неустойчивость в колебательных и волновых системах).2) Неустойчивость в газовой или жидкой среде, находящейся в поле силы тяжести F и пронизываемой потоком тепла с компонентом в направлении, противоположном F. Эта К. н. объясняется появлением подъёмной (архимедовой) силы при случайных вертикальных перемещениях элемента вещества. Давление Р _э в элементе быстро сравнивается с давлением среды Р, поэтому темп-ры и плотности в поднимающемся элементе ( Т _э, 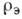)и в среде ( Т, 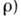удовлетворяют одному из двух условий: Т _э<Т, 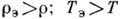.В первом случае архимедова сила возвращает элемент обратно, а во втором - стремится вытолкнуть его ещё выше вверх, что и приводит к К. н. Если пренебречь обменом энергией между элементом и средой (быстрый подъём элемента), то при его перемещениях и Т _э (Р и Т _э) связаны условием адиабатич-ности (см. 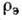Адиабата). При этом изменение темп-ры элемента с высотой 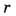(т. е. в направлении, противоположном F )описывается т. н. адиабатич. градиентом:

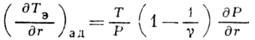
где 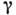- показатель адиабаты. В этом случае для возникновения К. н. необходимо, чтобы абс. величина градиента темп-ры среды была больше абс. величины адиабатич. градиента. Условие возникновения К. н. удобно записать через логарифмич. производные:

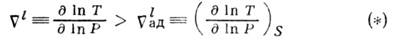
(индекс S означает, что производная берётся при постоянной энтропии 5). В химически неоднородной среде (при наличии градиента ср. молекулярной масса. 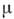)вместо 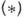обычно используется условие

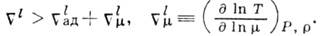
Диссипативные процессы - вязкость и теплопроводность - стремятся сравнять темп-ру в поднимающемся элементе с темп-рой окружающей среды. Их стабилизирующее влияние существенно только для мелкомасштабных движений. Вблизи границы потери устойчивости конвективные движения носят регулярный (ламинарный) характер. Когда Рейнолъдса число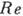= = 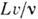(L - характерный размер, 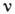- кинематич. вязкость, 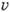- скорость конвективных движений) превысит 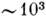, произойдёт турбулизация конвективных движений.

Конвективные движения, возникающие в результате К. н., широко распространены в природе: ею вызываются разл. движения в атмосфере Земли и др. планет; конвективные движения в ядре Земли, по-видимому, ответственны за поддержание магн. поля нашей планеты. Области с пост. конвективными движениями имеются почти во всех звёздах (см. Конвективная зона )В звёздах и часто в атмосферах планет конвекция является турбулентной (большие L).

Теоретич. описание конвективных движений представляет собой очень сложную задачу, ввиду необходимости решения двух- и трёхмерных нестационарных гидродинамич. ур-ний. При рассмотрении конвективно-го переноса энергии внутри звёзд обычно используется упрощённое описание - теория длины перемешивания, к-рая предполагает, что движущийся вертикально конвективный элемент в среднем на расстоянии l полностью передаёт избыток своей энергии окружающей среде. Длина перемешивания l обычно принимается прибл. равной характерной шкале высот по давлению:

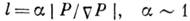
Поток энергии выражается соотношением

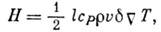
где 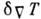означает разность между фактич. и адиабатич. градиентами темп-ры, 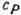- теплоёмкость при пост. давлени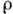и, и 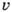- плотность и скорость конвективного элемента. Характерная скорость конвективного элемента получается из условия равенства кинетич. энергии элемента работе подъёмной силы на длине перемешивания:

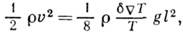
где g - ускорение силы тяжести.

Лит.: Ландау Л.- Д., Л и ф ш и ц Е. М., Механика сплошных сред, 2 изд., М., 1954; Шварцшильд М., Строение и эволюция звезд, пер. с англ., М., 1961; Голицын Г. С., Введение в динамику планетных атмосфер. Л., 1973. Г. С. Бисноватый-Коган.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.