- ЛОРЕНЦА - ДИРАКА УРАВНЕНИЕ
- ЛОРЕНЦА - ДИРАКА УРАВНЕНИЕ
-
- релятивистское ур-ние движения классич. точечной заряж. частицы в эл.-магн. поле, учитывающее силу реакции, с к-рой действует на частицу её собств. поле излучения. Эта сила реакции исследовалась до возникновения теории относительности X. А. Лоренцем (1892), релятивистски инвариантное рассмотрение вопроса проведено П. А. М. Дираком (Р. А. М. Dirac, 1938). Л.-Д. у. имеет вид (в СГС)
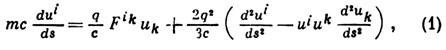
где
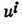 - 4-вектор скорости частицы, q и т - её заряд и масса,
- 4-вектор скорости частицы, q и т - её заряд и масса, 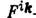 -тензор внеш. эл.-магн. поля,
-тензор внеш. эл.-магн. поля,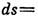
 ,
, 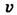 - трёхмерная скорость частицы.
- трёхмерная скорость частицы.
В системе отсчёта, в к-рой
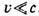 , (1) можно записать в виде
, (1) можно записать в виде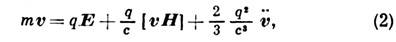
где точка обозначает дифференцирование по времени, Е и H - векторы внешних электрич. и магн. полей. Первые два члена в (2) представляют собой Лоренца силу, третий член - силу реакции излучения (называемую также силой торможения излучением или силой радиац. трения). Ур-ния (1) и (2) учитывают, что частица, движущаяся с ускорением, излучает в единицу времени энергию, равную
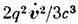 (в системе отсчёта, где v=0). Из (1) следует выражение, полученное ранее (из условия баланса энергии и импульса) М. Абрагамом (М. Abraham, 1904) для силы торможения излучением, справедливое при любых скоростях частицы:
(в системе отсчёта, где v=0). Из (1) следует выражение, полученное ранее (из условия баланса энергии и импульса) М. Абрагамом (М. Abraham, 1904) для силы торможения излучением, справедливое при любых скоростях частицы:
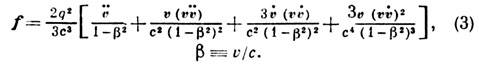
В задачах классич. электродинамики сила торможения излучением
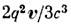 мала (в системе покоя частицы) по сравнению с силой Лоренца. Условия малости силы торможения излучением можно записать в виде
мала (в системе покоя частицы) по сравнению с силой Лоренца. Условия малости силы торможения излучением можно записать в виде
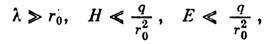
где
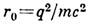 - классич. радиус частицы (см. Классический радиус электрона),
- классич. радиус частицы (см. Классический радиус электрона),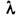 - характерная длина волны поля излучения. В области применимости классич. электродинамики эти условия всегда выполняются, т. к. уже при значительно больших длинах волн
- характерная длина волны поля излучения. В области применимости классич. электродинамики эти условия всегда выполняются, т. к. уже при значительно больших длинах волн 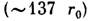 и значительно меньших полях
и значительно меньших полях 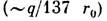 начинают проявляться квантовые эффекты.
начинают проявляться квантовые эффекты.
В отсутствие внеш. поля ур-ние (2), кроме физически разумного решения
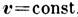 , имеет также решение
, имеет также решение 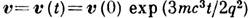 , описывающее самоускоряющуюся частицу. Обычно считается [1], что существование таких абсурдных решений Л.-Д. у. указывает на серьёзную и неустранимую внутр. трудность классич. электродинамики, связанную с бесконечностью эл.-магн. массы точечного заряда. Однако ситуация, когда не все решения нек-рого ур-ния имеют физ. смысл, является довольно общей [2]. Напр., из волновых решений ур-ний Максвелла обычно используются только запаздывающие потенциалы, а для описания финитного движения в квантовой механике пригодны только нормируемые решения ур-ния Шрёдингера. Не существует принципиальных затруднений, препятствующих отбору физически разумных решений Л.-Д. у. даже в случаях, когда сила радиац. трения не мала по сравнению с внеш. силой.
, описывающее самоускоряющуюся частицу. Обычно считается [1], что существование таких абсурдных решений Л.-Д. у. указывает на серьёзную и неустранимую внутр. трудность классич. электродинамики, связанную с бесконечностью эл.-магн. массы точечного заряда. Однако ситуация, когда не все решения нек-рого ур-ния имеют физ. смысл, является довольно общей [2]. Напр., из волновых решений ур-ний Максвелла обычно используются только запаздывающие потенциалы, а для описания финитного движения в квантовой механике пригодны только нормируемые решения ур-ния Шрёдингера. Не существует принципиальных затруднений, препятствующих отбору физически разумных решений Л.-Д. у. даже в случаях, когда сила радиац. трения не мала по сравнению с внеш. силой.
Ещё одной, парадоксальной на первый взгляд, особенностью силы радиац. трения является обращение её в нуль при равномерно ускоренном движении. В релятивистской теории равномерно ускоренное движение - это движение, при к-ром ускорение частицы постоянно в сопутствующей (собственной) системе отсчёта. Это означает, что 4-вектор скорости частицы ui удовлетворяет условию

где
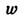 - инвариантное ускорение, т. е. ускорение в сопутствующей системе отсчёта, в к-рой условию (4) соответствуют соотношения
- инвариантное ускорение, т. е. ускорение в сопутствующей системе отсчёта, в к-рой условию (4) соответствуют соотношения

Условия (4) и (5) приводят к исчезновению силы радиац. трения в ур-ниях (1) и (2). Т. к. частица, движущаяся с постоянным инвариантным ускорением, за время t излучает энергию
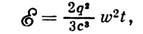
то возникает вопрос: как частица может излучать, если радиац. трение равно нулю? Понять, как это происходит, можно, рассмотрев конкретную физ. ситуацию [3]. Релятивистское равноускоренное движение с инвариантным ускорением
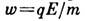 реализуется в случае движения заряж. частицы вдоль пост. однородного электрич. поля Е. Пусть поле заключено в объёме между пластинами конденсатора, тогда частица, двигавшаяся с пост. скоростью, попадает в электрич. поле в момент t1 и покидает его в момент t2. Т. к. ускорение при этом изменяется скачкообразно (формально), то сила радиац. трения (3) в эти моменты времени обращается в бесконечность (в рамках принятой формализации), причём так, что работа этой силы в точности равна излучённой энергии.
реализуется в случае движения заряж. частицы вдоль пост. однородного электрич. поля Е. Пусть поле заключено в объёме между пластинами конденсатора, тогда частица, двигавшаяся с пост. скоростью, попадает в электрич. поле в момент t1 и покидает его в момент t2. Т. к. ускорение при этом изменяется скачкообразно (формально), то сила радиац. трения (3) в эти моменты времени обращается в бесконечность (в рамках принятой формализации), причём так, что работа этой силы в точности равна излучённой энергии.
Лит.:1) Ландау Л. Д., Лифшиц Е, М., Теория поля, 7 изд., М., 1988; 2) Клепиков Н. П., Силы торможения излучением и излучение заряженных частиц, "УФН", 1985, т. 146, с. 317; 3) Гинзбург В. Л., Теоретическая физика и астрофизика, 3 изд., М., 1987. Ю. П. Степан овечий.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
