ЛЕЖАНДРА ФУНКЦИИ — функции, являющиеся решениями дифференциального уравнения Лежандра: где произвольные числа. Если v=0,1,2,..., а то ограниченные на [ 1, 1] решения уравнения (*) наз. Лежандра многочленами;при целых ограниченные на [ 1,1] решения уравнения (*) наз … Математическая энциклопедия
ЛЕЖАНДРА МНОГОЧЛЕНЫ — сферические многочлены, многочлены, ортогональные на сегменте [ 1,1] с единичным весом Стандартизованные Л. м. определяются Родрига формулой и имеют представление Наиболее употребительны формулы Л. м. можно определить как коэффициенты разложения… … Математическая энциклопедия
ЛЕЖАНДРА УРАВНЕНИЕ — см. Лежандра функции … Математическая энциклопедия
ЛЕЖАНДРА ПРЕОБРАЗОВАНИЕ — 1) Преобразование математич. анализа, осуществляющее двойственность между объектами в дуальных пространствах (наряду с проективной двойственностью в аналитич. еометрии и полярной двойственностью в выпуклой геометрии). Пусть гладкая функция,… … Математическая энциклопедия
Лежандра многочлены — сферические многочлены, специальная система многочленов последовательно возрастающих степеней. Впервые рассматривалась А. Лежандром и П. Лапласом (в 1782 85) независимо друг от друга. Для n = 0,1,2,... Л. м. Р (х) могут быть определены… … Большая советская энциклопедия
ЛЕЖАНДРА УСЛОВИЕ — необходимое условие для решения простейшей задачи вариационного исчисления, предложенное А. Лежандром (A. Legendre, 1786): для того чтобы кривая у 0 (х). доставляла минимум функционалу необходимо, чтобы во всех точках кривой у(х).вторая… … Математическая энциклопедия
Преобразование Лежандра — для заданной функции F(x) это построение функции F*(p), двойственной ей по Юнгу. Если исходная функция была определена на векторном пространстве V, её преобразованием Лежандра будет функция, определённая на сопряжённом пространстве V*, т.е. на… … Википедия
СПЕЦИАЛЬНЫЕ ФУНКЦИИ — в широком смысле совокупность отдельных классов функций, возникающих при решении как теоретических, так и прикладных задач в самых различных разделах математики. В узком смысле под С. ф. подразумеваются С. ф. математич. физики, к рые появляются… … Математическая энциклопедия
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
Многочлен Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
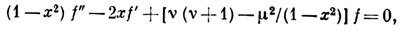
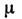и 
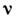- произвольные параметры. Если 
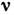- целое положит. число,
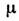=0, Л. ф. вырождаются в полиномы Лежандра. При целых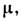 
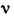и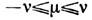 
получаются присоединённые полиномы Лежандра (см. Ортогональные полиномы). В общем случае вводят Л. ф. первого 
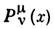и второго 
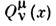рода, они выражаются через гипергеометрическую функцию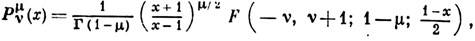
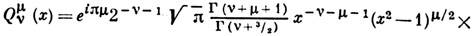
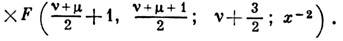
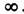, Л. ф. встречаются, напр., при решении ур-ния Лапласа, волнового ур-ния или ур-ния диффузии в сферич. координатах. Л. ф. 
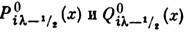наз. функциями конуса.