КРИВИЗНЫ ТЕНЗОР

КРИВИЗНЫ ТЕНЗОР

(Римана тензор) - локальная характеристика кривизны в римановой геометрии. К. т. определяют с помощью процедуры параллельного переноса вектора вдоль замкнутой кривой в римановом пространстве. Параллельным (ковариантно постоянным) вдоль кривой 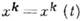наз. векторное поле Fⁱ (х), для к-рого обращается в нуль ковариантная производная 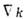по направлению скорости кривой 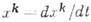: 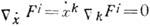. В евклидовой геометрии существуют координаты, в к-рых ковариантная производная 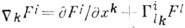сводится к обычной (а Кристоффеля символы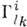равны нулю), поэтому результат переноса не меняет вектора и не зависит от кривой. В римановой геометрии таких координат не существует, полученный в результате переноса вектор отличен от первоначального, причём отличие 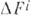в пределе малой кривой пропорц. площади 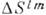ограниченной ею поверхности: 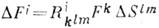, где К. т. 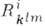равен

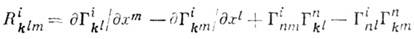
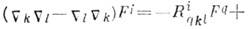
Равенство нулю всех компонент К. т. в каждой точке пространства необходимо и достаточно для того, чтобы это пространство было евклидовым. С К. т. связана некоммутативность ковариантных производных; для общих связностей 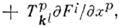где 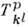-тензор кручения. Если перейти от смешанных компонент К. т. 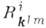к его ковариантным компонентам 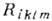по правилу 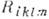= =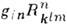, где g_in - метрический тензор, то для 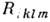имеет место равенство

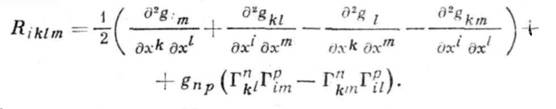
Отсюда вытекают след. свойства К. т.:

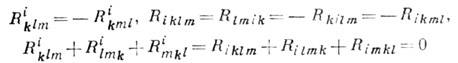
(тождество Риччи),

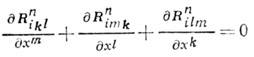
(тождество Бьянки).

Полное число N разных, не равных нулю, компонент К. т. в n -мерном римановом пространстве равно N= 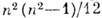. Из К. т. путём свёртывания R_k = = 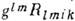получается Риччи тензор R_ik. Наконец, свёртывание R_ik даёт инвариант .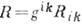, наз. скалярной кривизной пространства.

Лит.: Фок В. А., Теория пространства, времени и тя-. готения, 2 изд., М., 1961; Дубровин Б. А., Новиков С. П., Фоменко А. Т., Современная геометрия, 2 изд.. М . 1986. В. И. Алхимов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.