ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА

ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА

(ТЭИ) - тензор второго ранга, описывающий плотность и поток энергии и импульса полей материи, определяющий взаимодействие этих полей с гравитац. полем. В классич. теории ТЭИ 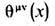выражается через вариационную производную по метрическому тензору g_mv (х )в точке х пространства-времени от инвариантного относительно замен координат функционала действия S:

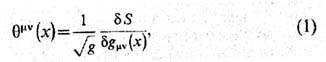
где 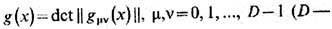размерность пространства-времени). Тензор, определяемый по ф-ле (1), очевидно симметричен. В ур-ниях Эйнштейна ТЭИ входит в качестве внеш. источника гравитац. поля: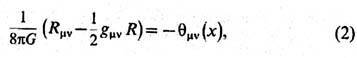

где R_mv -Риччи тензор, 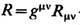-скалярная кривизна (используется система единиц, в к-рой с=1),

В плоском пространстве-времени симметрия системы относительно сдвигов (или, иначе, существование инвариантного относительно замен координат и зависящего от метрики функционала действия) приводит к локальному сохранению энергии и импульса (см, Нётер теорема):

где

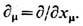
Следствием (3) является, в частности, сохранение вектора полных энергии и импульса системы. Величина

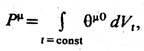
где dV_t -элемент объёма гиперповерхности пост. времени, не зависит от выбора гиперповерхности, т. е. dP^m/dt =0.

Для непрерывного распределения материи с плотностью r и потоком 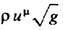ТЭИ даётся выражением

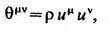
где ii^m-4-скорость.

В квантовой теории поля в простейших случаях свободного скалярного поля (а), свободного фермионного поля ( Дирака поля )(б) и Янга- Миллса поля (в) ТЭИ в стандартных обозначениях имеют вид

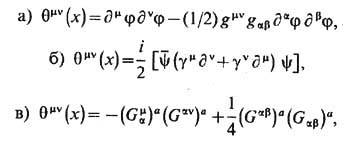
где j -скаляоное поле. y - фермионное поле и 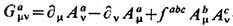- тензор напряжённости поля Янга -Миллса, принимающего значения в Ли алгебре со структурными константами f^{ab с}.

Через ТЭИ также выражаются токи, связанные с др. пространственными симметриями. Тензор момента импульса M^ab_m и дилатац. ток D_m, сохранение к-рых отвечает соответственно симметриям системы относительно глобальных вращений и растяжения, след, образом связаны с ТЭИ(1)

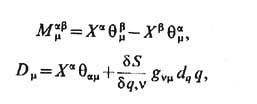
где d_q равно разности между канонич. размерностью (см. в ст. Аномальная размерность )и порядком тензорного поля q. Сохранение момента импульса гарантируется симметричностью ТЭИ. Сохранение же дилатац. тока в случае, когда d_q =0, эквивалентно условию нулевого следа ТЭИ.

ТЭИ допускает модификации, не нарушающие условия сохранения (3). Модифицированные ТЭИ отличаются на дивергенцию антисимметричного 3-тензора:

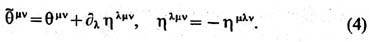
При условии достаточно быстрого убывания h ^lmv на бесконечности новый ТЭИ приводит к тому же вектору полных энергии и импульса системы. Модифицированные ТЭИ могут возникать при добавлении к действию членов, исчезающих в плоском пространстве. Примером модифицированного ТЭИ может служить канонич. ТЭИ

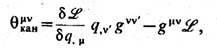
являющийся сохраняющимся током теории, отвечающим, согласно первой теореме Нётер, симметриям относительно сдвигов в пространстве-времени 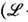-лагранжиан теории). Канонич. ТЭИ в общем случае не является симметричным, и его связь с тензором момента импульса не столь проста.

Иногда полезно рассматривать конформный ТЭИ, получающийся из (1) с помощью (4) и удовлетворяющий условию нулевого следа (q _конф)_m^m=0. Для полей Янга - Миллса и безмассовых фермионов в размерности D =4конформный ТЭИ совпадает с ТЭИ (1), что связано с конформной инвариантностью соответствующих теорий. В случае безмассового скалярного поля в D -мерном пространстве-времени конформный ТЭИ имеет вид

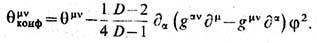
С ним связан сохраняющийся дилатац. ток 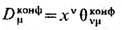Существование конформного ТЭИ означает, что теория может быть сделана конформно инвариантной добавлением к действию членов, исчезающих в плоском пространстве. В случае скалярного поля это достигается след. модификацией функционала действия:

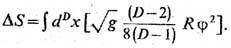
В присутствии гравитац. поля (в искривлённом пространстве-времени) ТЭИ материи уже не удовлетворяет условию локального сохранения (3). Вместо этого из ур-ний гравитац. поля и тождества Бьянки (см., напр., Кривизны тензор )следует ур-ние

где 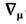- ковариантная производная. Отличие (5) от (3) приводит к нарушению сохранения энергии и импульса только полей материи. Полный же ТЭИ материи и гравитации, определяемый согласно (1), равен нулю в силу ур-ний движения и сохраняется автоматически.

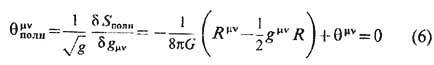
Это свойство является общим для теорий, обладающих локальной симметрией. Согласно второй теореме Нётер, полный ток в таких теориях равен нулю. Более того, оказывается, что невозможно модифицировать гравитац. часть выражения (6) так, чтобы полный ТЭИ был отличен от нуля и удовлетворял бы условиям сохранения (3). Т. о., в присутствии гравитац. поля нет содержательного понятия полного ТЭИ.

В нек-рых спец. случаях оказывается разумным ввести, используя преобразование (4), псевдотензор энергии-импульса гравитац. поля, являющийся тензором только относительно линейных преобразований координат. Так, если материя сосредоточена в ограниченной области пространства и на бесконечности пространство является плоским, симметричный псевдотензор энергии-импульса получается модификацией гравитац. части тензора (6), Напр.,

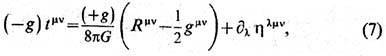
где h^lmv даётся след. выражением:

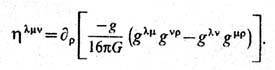
Так как t^mv не является тензором, ковариантное понятие плотности энергии и импульса не определено (напр., преобразованиями координат t^mv может быть сделан равным нулю в любой данной точке). Однако вектор полных энергии и импульса системы

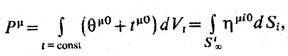
где S^t_x -бесконечно удаленная поверхность, сохраняется во времени и не зависит от выбора координат пространственно временной "трубки", в к-рой сосредоточена мате-рия Т о , псевдотензор (7) определяет разумное понятие потных энергии и импульса Отметим однако, что в теории гравитации использование нековариантных. объектов типа (7) приносит мало пользы

В квантовой теории поля ТЭИ становится оператором, генерирующим общекоординатные преобразования При использовании общековариантной относительно преобразований координат регуляризации (напр , размерной или регуляризации по Паули - Вилларсу), в силу операторного аналога закона сохранения ТЭИ (3), одновременные перестановочные соотношения для компонент ТЭИ в квантовой теории не перенормируются (см Перенормировки в КТП) и совпадают по форме с классическими Пуассона скобками В частности, оператор q^mv не приобретает ано-мальных размерностей В нек-рых случаях однако, оказывается необходимым использовать регуляризацию, нарушающую общую ковариантность, но сохраняющую другие симметрии теории, напр киральную или дилатационную, поскольку одновременно сохранять все симметрии на квантовом уровне не удается Примерами могут служить теории киральных фермионов (см Кираль ность )со спинами 3/2 и 1/2 в пространствах D =4k +2(k = 0, 1, 2, ) измерении, имеющие гравитац аномалию (см Аномалии в квантовой теории поля) В этих теориях на квантовом уровне закон сохранения (3) модифицируется, и в перестановочных соотношениях появляются дополнительные слагаемые Так, для ТЭИ фермионов со спином s=1/2 в D = 2 выполняются след перестановочные соотношения, отличающиеся от классич скобок Пуассона членом, содержащим производную третьего порядка

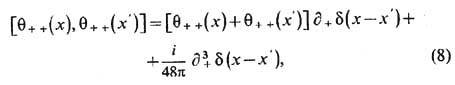
где 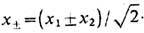-координаты светового конуса в двумерном пространстве-времени и В теориях, имеющих гравитац аномалию, 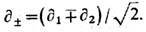возникают трудности при описании их взаимодействия с гравитацией и обычно накладываются условия сокращения аномальных членов в перестановочных соотношениях (8) для полного ТЭИ

Наиболее часто встречающейся аномалией, связанной с ГЭИ является аномалия, отвечающая нарушению классич. масштабной инвариантности В перенормированнои теории масштабная инвариантность нарушается зависимостью констант связи oт точки нормировки, определяемой бета-функцией (b) Имеется след ф-ла для среднего от дивергенции дилатац тока, равного следу ТЭИ

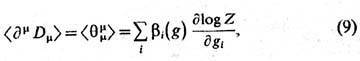
где Z- статистич сумма теории, g_i- константы связи, < > -символ усреднения по вакууму

В квантовой хромодинамике (9) сводится к утверждению о связи следа ТЭИ и глюонного конденсата

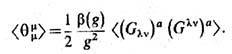
Используя изотропность распределения энергии и импульса можно также связать плотность энергии вакуума в КХД с величиной глюонного конденсата

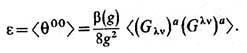
Лит.: Ландау Л. <Д. Лифшиц Е. <М, Теория поля, 7 изд М , 1988 Волошин М. Б, Те r Мартиросян К А, Теория калибровочных взаимодействий элементарных частиц М 1984 Ицик-сон К, Зюбер Ж Б, Квантовая теория поля пер с англ , т 1-2, М, 1984 Aivarez-Gaume L Witten Ь Gravitational anomalies 'Nucl Phys Sei В 1984, v 234 p 269 А А Герасимов

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.