КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ

КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ

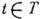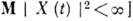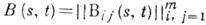случайного процесса 2526-27.jpg - ф-ция В (s, t) = М[ Х (s) - -MX (s)].[X(t) - MX (t)]*, s, 2526-28.jpg, [здесь MX (t) - первый момент процесса, * означает комплексное сопряжение; предполагается, что 2526-29.jpg. В случае векторного процесса 2526-30.jpg К. ф. наз корреляционная матрица 2526-31.jpg, где Bij(s, t) =2526-32.jpg - взаимная К. ф. процессов Xi и Xj, В ii наз . иногда автокорреляционной функцией. Характеристич. свойство К. ф.- её положит. определённость: для любых t1, . . ., tn2526-33.jpg Т икомплексных с1 . . ., с т: . Для процесса с

независимыми значениями 2526-34.jpg В (s, t)=0при s2526-35.jpgt. Для стационарных в широком смысле процессов К. ф. зависит лишь от разности t-s: В (s, t) = R(t-s). Если при этом процесс непрерывен в среднем квадратическом, т. е. М 2526-36.jpg при 2526-37.jpg, то К. ф. R(t). непрерывна и допускает представление R(t) = 2526-38.jpg , где F - спектральная мера процесса, а 2526-39.jpg пробегает интервал 2526-40.jpg , если Т=(2526-41.jpg), либо [2526-42.jpg], если Т={. . .,- 1, 0, 1, . . .} (см. также Винера - Хинчина теорема).

К. ф.- простая, но полезная характеристика случайного процесса. Распределение гауссовой случайной функции X (t )полностью определяется её К. ф. и средним MX (t); в общем случае это заведомо не так. В то же время К. ф. вполне описывает процесс как кривую в гильбертовом пространстве интегрируемых в квадрате ф-ций на вероятностном пространстве, на к-ром задан процесс (см. Вероятностей теория), позволяет судить о таких его свойствах, как непрерывность, дифференцируемость и интегрируемость в среднем квадратическом и т. п. Условия на скорость убывания К. ф. при 2526-43.jpg используют в предельных теоремах для случайных процессов.

Лит.: Гихман И. И., Скороход А. В., Введение в теорию случайных процессов, 2 изд., М., 1977; Введение в статистическую радиофизику, ч. 1 - Рытов С. М., Случайные процессы, М., 1976. К. А. Боровков.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. . 1988.


.

Игры ⚽ Нужно решить контрольную?

Полезное


Смотреть что такое "КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ" в других словарях:

  • корреляционная функция — Ндп. автокорреляционная функция Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время. Примечание Корреляционная функция характеризует… …   Справочник технического переводчика

  • Корреляционная функция — Корреляционная функция  функция времени или пространственных координат, которая задает корреляцию в системах со случайными процессами. Зависящая от времени корреляция двух случайных функций X(t) и Y(t) определяется как: , где угловые скобки… …   Википедия

  • КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ — в статистической физике ф ция, определяющая вероятность относит. расположения комплекса из s любых молекул жидкости или газа; при s=2 К. ф. наз. парной или бинарной. Появление корреляций в расположении молекул среды связано с тем, что в ближайшем …   Физическая энциклопедия

  • Корреляционная функция — 24. Корреляционная функция Ндп. Автокорреляционная функция Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время. Примечание.… …   Словарь-справочник терминов нормативно-технической документации

  • КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ — действительного случайного процесса функция аргументов t, . определяемая равенством Для того чтобы К. ф. была определена, следует предположить, что процесс X(t).при всех имеет конечный второй момент Параметр tпробегает здесь некоторое… …   Математическая энциклопедия

  • КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ СЛУЧАЙНОГО ПРОЦЕССА — см. Функция корреляционная случайного процесса. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 …   Геологическая энциклопедия

  • Корреляционная функция случайного процесса — 16. Корреляционная функция случайного процесса Функция двух переменных t и и, равная ковариационной функции центрированного случайного процесса Rξ (t, u) = M{[ξ(t) m1]×[ξ(u) m2]}, t,uЄT Источник …   Словарь-справочник терминов нормативно-технической документации

  • КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ — в статистической механике функция, описывающая влияние частиц или групп частиц друг на друга и эффекты взаимодействия подсистем рассматриваемой системы. В классической статистич. механике К. ф. G2(l, 2), G3(l, 2.3), ... определяются соотношениями …   Математическая энциклопедия

  • Корреляционная функция — 1. Функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время Употребляется в документе: ГОСТ 16465 70 Сигналы радиотехнические измерительные.… …   Телекоммуникационный словарь

  • Нормированная корреляционная функция — 25. Нормированная корреляционная функция Ндп. Коэффициент корреляции Функция, равная отношению корреляционной функции случайного сигнала к его дисперсии Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и определения …   Словарь-справочник терминов нормативно-технической документации


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»