КОРРЕЛЯЦИОННАЯ ЭНЕРГИЯ

КОРРЕЛЯЦИОННАЯ ЭНЕРГИЯ

- энергия ниж. энергетич. состояния газа электронов ( ферми-газа )за вычетом их ср. кинетич. энергии ( ферми-энергии )иэнергии обменного взаимодействия. В общем случае К. э. представляет собой разность энергии осн. состояния системы ферми-частиц и её значения, определённого в приближении Хартри - Фока (см. Хартри - Фока метод).

Согласно Паули принципу, два электрона с одинаковым направлением спина не могут находиться в одной ячейке фазового пространства, что эквивалентно отталкиванию между ними. Это приводит к тому, что ср. кинетич. энергия электронного газа даже при нулевой темп-ре отлична от нуля и в случае газа большой плотности даёт осн. вклад в энергию системы. Принцип Паули приводит также к корреляции во взаимном расположении электронов с параллельными спинами, к-рой соответствует обменная энергия. Вклад этого типа корреляции в энергию системы можно учесть с помощью теории возмущения в её первом приближении. Кроме того, существует корреляция электронов с противоположно направленными спинами вследствие кулоновского отталкивания между ними, она обусловливает свой специфич. вклад в энергию системы - т. н. К. э. Этот квантовомеханич. эффект можно приписать существованию в системе "корреляц. дырки" (корреляц. разрежения), в отличие от "фермиевской дырки", обусловленной принципом Паули.

К. э. нельзя учесть в рамках обычной теории возмущений: второе приближение для энергии электронного газа приводит к логарифмически расходящимся выражениям, т. к. влияние кулоновского взаимодействия вследствие его дальнодействия нельзя считать малым. Расходимость остаётся и в более высоких приближениях. Для вычисления второго и высших приближений для энергии электронного газа, т. е. для вычисления К. э., необходимо пользоваться усовершенствованной формой теории возмущений.

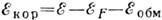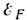К. э. электронного газа, по Ю. Вигнеру (Е. Wigner, 1938), определяется ф-лой , где - ср. кинетич. энергия электронного газа при Т=0К, рассчитанная на один электрон в первом приближении теории возмущений:

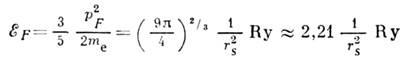
[здесь P_F- ферми-импульс электронов, r_s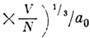⁼( - ср. расстояние между электронами в единицах боровского радиуса 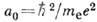, R _у= 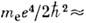13,55 эВ (ридберг)];.- ср. энергия кулоновского взаимодействия в электронном газе на один электрон:

Положит. заряд ионов (если рассматривают газ свободных электронов в металле) предполагается равномерно распределённым по объёму, т. е. влияние крис-таллич. решётки не учитывается.

Для случая малой плотности газа электронов Вигнер принял, что электроны образуют в пространстве решётку, н получил след. разложение для К. э.:

где U₁ = -0,88.

Для электронного газа большой плотности (r_s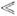1) Вигнер вычислил К. э. вариац. методом. Интерполируя между этими двумя пределами, Вигнер нашёл

Случай большой плотности может быть исследован более строго. Суммирование главных, дающих наибольшую степень расходимости, членов теории возмущений при r_s1 приводит к разложению

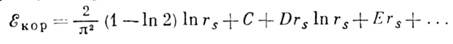
Первый логарифмич. член разложения был определён Маке (Macke, 1950) на основе теории возмущений, а затем получен Д. Бомом и Д. Пайнсом (D. Bohm, D. Pines, 1953) методом коллективных переменных. Пост. член С= - 0,096 был вычислен М. Гелл-Маном и К. Бракнером (М. Gell-Mann, К. Brueckner, 1957) методом суммирования Фейнмана диаграмм, ими же была оценена величина третьего и четвёртого членов разложения. К. э. была также вычислена Ф. Нозьером (Ph. Nozieres) и Д. Пайнсом в 1958 методом коллективных переменных.

Для реальных металлов плотности электронного газа соответствуют значениям r_s в интервале 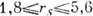, т. е. промежуточным плотностям. Для оценки К. э . щелочных металлов можно применить модель свободного электронного газа, без учёта кристаллич. решётки.

Пренебрежение Н. э. приводит к неверной оценке роли корреляций электронов с параллельными спинами (поскольку при этом совершенно не учитывается корреляция электронов с антипараллельными спинами). Без учёта К. э. при очень малых плотностях оказывается возможным ферромагнетизм электронного газа, учёт же К. э. делает его невозможным.

Лит.: Пайнс Д., Элементарные возбуждения в твердых телах, пер. с англ., М., 1965, гл. 3, p 3; Марч Н., Янг У.. Сампантхар С., Проблема многих тел в квантовой механике, пер. с англ., М., 1969, гл. 5, Приложение 4.

Д. Н. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.