- КИРАЛЬНЫЕ ПОЛЯ
- КИРАЛЬНЫЕ ПОЛЯ
-
- поля, преобразующиеся по определ. представлению группы киральных преобразований - преобразований симметрии, не коммутирующих с операцией отражения пространственных координат ( пространственной инверсии), т. е. не обладающих определ. четностью. Конкретный вид киральных преобразований может быть разным, в частности он зависит от спин-тензорной и изотопич. структуры поля. Классич. примером киральных преобразований могут служить вращения дираковского спинора (см. Дирака поле )с фазой, пропорциональной
, где 
- Дирака матрица (см. ниже). Четырёхкомпонентное поле Дирака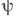 
можно представить в виде композиции двух двухкомпонентных, или вейлевских, спиноров 
(
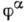= = 1, 2):
где индексы L и R означают левый и правый вейлевский спинор. Соответственно поля
называют левым и правым полями или полями левой и правой частицы. Эта терминология отражает тот факт, что при нулевой массе частицы поля
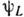или 
имеют определённую (левую или правую) спиралъностъ. Левый вейлевский спинор определён законом преобразования при лоренцовых вращениях системы отсчёта х в систему отсчёта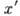 
:
Здесь
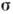- Паули матрицы,
- векторы, параметризующие преобразования Лоренца: 
- вектор в направлении скорости пространственной системы координат 
относительно системы координат 
- вектор вращения системы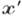 
относительно 
. При отражении пространственных координат 
, 
, поэтому левый спинор переходит в правый, к-рый задан своим законом преобразования, отличающимся от (1) знаком перед вектором 
:
Действие матрицы
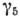на правый и левый спиноры отличается знаком:
где I - единичная матрица 2
2. Киральным преобразованием дираковского спинора 
служит операция
где
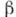- параметр преобразований. Поля 
и 
являются при этом К. п. и преобразуются по закону:
Если имеется неск. дираковских полей, отвечающих, напр., разл. кваркам, то киральные преобразования могут включать и изменение сорта (аромата) кварка, напр. изотопич. вращения (см. Изотопическая инвариантность).
Киральные преобразования можно определять и для бозонных полей. Если есть, напр., скалярное поле а и псевдоскалярное поле
, то киральным является преобразование вида
где
- параметр преобразования. При наличии неск. подобных полей (напр., полей 
) киральные преобразования также могут включать изменение сорта частиц.
Киральные преобразования особенно интересны в тех случаях, когда соответствующий лагранжиан инвариантен относительно таких преобразований.
Лит.: Р а м о н П., Теория поля, пер. с англ., М., 1984.
В. И. Захаров.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
