СКИРМА МОДЕЛЬ

СКИРМА МОДЕЛЬ

- теоретич. модель для описания в рамках эффективнойнелинейной теории мезонных полей стабильных протяжённых частиц (барионов).Предложена в 1961 Т. X. Р. Скирмом [1, 2] и относится к нелинейным сигма-моделям. <С. м. обладает сохраняющимся независимо от ур-ний динамики модели топологическимзарядом, к-рый можно интерпретировать как барионное число, и т. н. <солитонным механизмом генерации спектра масс (см. Солитон). Согласногипотезе Скирма, барион трактуется как киральный солитон, возникающий врезультате коллективного возбуждения пионных полей. Появление таких возбужденийтесно связано с явлением спонтанного нарушения киральной симметрии (см. Спонтанное нарушение симметрии), подобно тому как включение магн. <поля, нарушающего изотропию пространства, приводит к спонтанной намагниченностиферромагнетика.

Осн. объектом С. м. является пеле g(x), принимающее значенияв многообразии группы SU(2 )и параметризуемое изовекторным полем 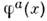(триплетом пионных полей):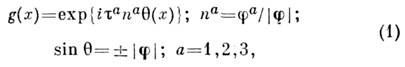

где 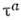- Паули матрицы, действующие в пространстве изотопич. спина;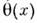- т. н. киральный угол; х= ( х ⁰= t, х). Модели, для к-рых поля принимают значения в нек-ром многообразии компактнойгруппы пли однородном пространстве, принято называть киральными. Поля (1),удовлетворяющие естеств. граничным условиям на пространственной бесконечности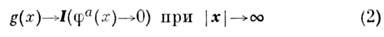

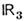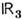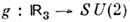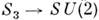(I - единичная 2x2 матрица) в фиксиров. момент времени t, можно рассматривать как отображения g вещественного трёхмерногопространства или трёхмерной сферы S₃[т. к., в силу(2),компактифицируется в сферу S₃] в группу SU(2) [ или ]. По отношению к непрерывной деформации (гомотопии), частным случаем к-ройявляется временная эволюция полевой системы, такие отображения разбиваютсяна классы эквивалентности, называемые гомотопическими классами. Каждыйгомотопич. класс является элементом гомотопич. группы 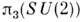и характеризуется значением гомотопич. инварианта - топологич. заряда Q.

Для явного вычисления Q удобно использовать левые киральные токи

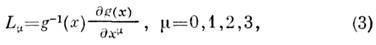
со значениями в Ли алгебре группы SU(2), в терминах к-рых

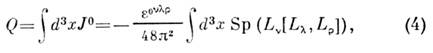
где J⁰ - временная компонента топологич. тока 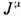,закон сохранения к-рого 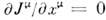выполняется тождественно без привлечения yp-ний динамики модели,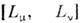- коммутатор левых киральных токов,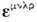- Леви-Чивиты символ (по повторяющемуся индексу предполагается суммирование).Наличие изоморфизма 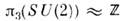,где 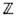-группа целых чисел, означает, что Q принимает на каждом классе целочисленноезначение н имеет смысл степени отображения, т. е. показывает, сколько раз SU(2)-многообразие обходится полем g(x )при однократном пробеганииточки x по физ. <пространству 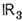Лагранжиан С. м. записывается через токи 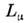в виде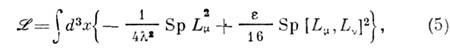

где 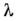и 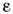- нек-рыепараметры. Первый член в выражении (5) - т. н. киральный лагранжиан Вайнберга, <к-рый в «древесном» приближении воспроизводит результаты алгебры токов для низкоэнергетич. динамики пионов. Добавление члена 4-го порядкапо 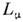(скирмовскогочлена) обеспечивает существование стабильных солитонных решений вследствиеналичия для функционала энергии 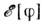С. м. оценки снизу через топологич. заряд (4):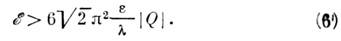

Ур-ния движения для С. м.

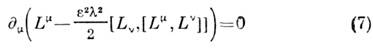
имеют вид локального закона сохранения величины типа изоспина. Отысканиеструктуры решений ур-ния (7) основывается на свойствах симметрии лагранжиана(5) и соответствующего функционала энергии 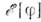Выражение (5) инвариантно относительно преобразований из игральной группы SU(2)_L х SU(2)_R, к-рые следующимобразом действуют на поля g(x):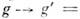=, где и и v - произвольные матрицы соответственно из SU(2)_L и SU(2)_R (индексы L н R помечают подгруппысоответственно левых и правых вращений). Но вакуумное состояние 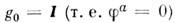такой инвариантностью не обладает до тех пор, пока 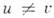Это означает, что С. м. принадлежит к классу нелинейных а-моделей со спонтаннонарушенной киральной симметрией. Из-за неинвариантности вакуума внутр. <симметрия конфигурац. пространства С. м. SU(2)_L.X SU(2)_R нарушается до подгруппы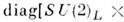 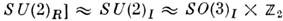,т. е. до группы изотопич. вращений. Поскольку нетривиальных SO(3)_I- инвариантныхполей не существует, то изотопич. вращения объединяются с пространственнымии в качестве группы инвариантности функционала 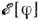рассматривается группа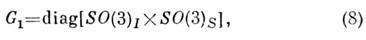

где SO(3)_S - группа пространственных вращений. Классинвариантных относительно (8) сферически-симметричных полей задаётся ф-лой

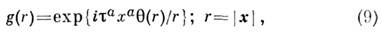
предложенной Скирмом [1]. В честь автора модели решение (9) с топологич. <зарядом Q =1 получило в литературе назв. с к и р м и о н. Энергия(масса) скирмиона записывается в виде

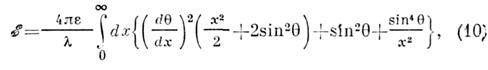
где положено , ф-ция 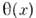подчиненаграничным условиям: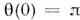;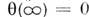.В силу неравенства (6) скирмион устойчив п, более того, реализует абс. <минимум энергии для полей с 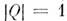,т. е. является осн. состоянием с наим. массой среди изовекторных полейс нетривиальным топологич. зарядом [3].

Все перечисленные выше свойства и дают основания для рассмотрения скирмионакак простейшей модели бариона. Для полей с топологич. зарядами 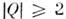группой инвариантности функционала энергии является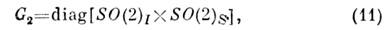

и абс. минимум 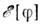реализуется в более широком классе аксиально-симметричных полей (см., напр.,[3]). В случае Q = 2 такие решения интерпретируются как дибарионы.

Дальнейшее развитие идея описания бариона как кирального солитона получилав работах Э. Виттена [4, 5], к-рый выявил связь между нелинейными 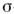-моделямисо спонтанно нарушенной киральной симметрией и нпзкоэнергетпч. приближением квантовой хромодинамики (КХД). Исходя из учёта симметрийных свойствфундам. лагранжиана КХД, Виттен рассмотрел SU(3)-обобщение С. м. <Это позволило ему построить явный вид двузначных функционалов, описывающихквантовомеханич. состояния в модели, и на этой основе конструктивно решитьвопрос о спине скирмиона, т. е. показать, в каком смысле скирмион можнотрактовать как фермион. Кроме того, в рамках квазиклассич. подхода удалоськачественно правильно воспроизвести спектроскопию адронов и рассчитатьих статич. свойства (магн. моменты, зарядовые радиусы, константы взаимодействийи т. д.). Разумные ответы получаются и при использовании С. м. для вычисленияразл. характеристик низкоэнергетич. процессов с участием барионов [6].

Т. <о., в целом С. м. качественно правильно передаёт гл. черты будущеймезонной теории, к-рая должна получаться из первооснов КХД, и в силу своейотносит, простоты может служить основой для апробации методов, предлагаемыхдля проведения расчётов в низкоэнергетич. области КХД.

Лит.:1) S k у r m е Т. Н. R., A non-linear field theory, «Proc.Roy. Soc.», 1961, v. A260, p. 127; 2) S k у r m e T. H. R., A unified fieldtheory of mesons and baryons, «Nucl. Phys.», 1962, v. 31, p. 556; 3) Ma x а н ь к о в В. Г., Рыбаков Ю. П., Санюк В. И., Модель Скирма и сильныевзаимодействия, УФН, 1992, т. 162, с. 1;4) Witten E., Global aspects ofcurrent algebra, «Nucl. Phys.», 1983, v. B223, p. 422; 5) Witten E., Currentalgebra, baryons and quark confinement, там же, р. 433; 6) Z a h e d I..В r о w n G. E., The Skyrme model, «Phys. Repts», 1986, v. 142, p. 1. В. <И. Санюк.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.