- КИРАЛЬНАЯ СИММЕТРИЯ
- КИРАЛЬНАЯ СИММЕТРИЯ
-
в квантовой теории поля (КТП), симметрия ур-ний движения, к-рая комбинируется из двух разл. симметрии: симметрии вз-ствия адронов относительно обычных преобразований в «изотопич. пр-ве» (см. ИЗОТОПИЧЕСКАЯ ИНВАРИАНТНОСТЬ) без изменения внутр. чётности и той же симметрии, но с изменением внутр. чётности. Т. о., преобразования К. с., кроме перемешивания состояний ч-ц с разл. электрич. зарядами, «перемешивают» и состояния с разной внутр. чётностью. К. с. явл. глобальной, т. е. не зависящей от точек пространства-времени. Такая инвариантность в случае ч-ц ненулевой массы не может быть связана ни с каким законом сохранения для фиксиров. системы ч-ц, а определяет лишь форму их вз-ствия, напр. форму вз-ствия нуклонов с псевдоскалярными пионами, испускание каждого из к-рых изменяет чётность системы. В этом смысле К. с. явл. динамич. симметрией. К. с.— один из примеров симметрии, приводящей к существенно нелинейной КТП (см. НЕЛИНЕЙНАЯ ТЕОРИЯ ПОЛЯ).Инвариантность относительно вращений в «изотопич. пр-ве» без изменения чётности связана с законом сохранения векторных токов (V), а с изменением чётности — с законом сохранения аксиальных токов (А) (см. ТОК). Сохранение векторного тока можно связать с сохранением полного электрич. заряда системы взаимодействующих ч-ц. В случае безмассовых спинорных (со спином 1/2) ч-ц, напр. нейтрино, сохранение аксиального тока можно связать с определ. законом сохранения — законом сохранения спиральности. Действительно, в случае безмассового спинорного поля, распространяющегося со скоростью света, спин квантов поля направлен либо против движения, либо в сторону движения. Соотв. различают левую и правую спиральности; 1-му случаю соответствует комбинация V-А токов частиц, 2-му — комбинация V+A, и эти комбинации должны сохраняться в отсутствие вз-ствия нейтрино с др. ч-цами. Однако если спинорная ч-ца имеет ненулевую массу покоя, то её спин не обязательно должен быть ориентирован по оси движения. Но во вз-ствиях с др. ч-цами это кач-во спиральности опять проявляется. Так, в слабом взаимодействии участвуют только лептоны с левыми спиральностями, а в сильном могут участвовать как левые (с левой спиральностью ч-ц) токи адронов (V-А), так и правые (V+A).Наряду с теорией поля, использующей лагранжев формализм с лагранжианами, удовлетворяющими требованиям К. с., для нахождения связей между вероятностями процессов с разл. числом взаимодействующих адронов используется т. н. а л г е б р а т о к о в— соотношения, связывающие коммутатор двух токов с самими токами. Она состоит из двух независимых алгебр: алгебры левых токов адронов (V-А) и алгебры правых токов адронов (V+A). Поскольку в этой теории имеется симметрия относительно правых и левых токов, данная симметрия и наз. киральной (от греч. cheir — рука).Киральная КТП описывает многочисл. процессы рассеяния и распада адронов при низких энергиях в хорошем согласии с эксперим. данными. Она имеет место и при описании процессов при очень высоких энергиях (напр., в модели партонов).К. с.— приближённая; она была бы точной, если бы масса псевдоскалярных пионов равнялась нулю. Поскольку же их масса отлична от нуля (хотя и существенно меньше массы барионов), аксиальные токи сохраняются лишь частично (степень несохранения пропорц. массе мезона, (см. АКСИАЛЬНОГО ТОКА ЧАСТИЧНОЕ СОХРАНЕНИЕ)).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- КИРАЛЬНАЯ СИММЕТРИЯ
-
(хиральная симметрия) (от греч. cheir - рука) сильного взаимодействия - приближённая симметрия сильного взаимодействия относительно преобразований, меняющих чётность (киральных преобразований; см. Киральные поля).
Согласно совр. точке зрения, сильное взаимодействие описывается квантовой хромодинамикой (КХД) - калибровочной теорией взаимодействия цветных кварков и глюонов. Лагранжиан КХД содержит поля кварков q=u, d,s, массы к-рых малы в масштабе масс, характерных для сильного взаимодействия (~1 ГэВ в системе единиц
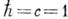 ). Более точная формулировка этого утверждения затруднена тем, что свободные кварки не существуют из-за явления т. н. конфайнмента ( удержания цвета). Можно, однако, говорить о массах кварков при квадратах переданного импульса, напр., порядка 1 ГэВ 2. Тогда массы примерно равны:
). Более точная формулировка этого утверждения затруднена тем, что свободные кварки не существуют из-за явления т. н. конфайнмента ( удержания цвета). Можно, однако, говорить о массах кварков при квадратах переданного импульса, напр., порядка 1 ГэВ 2. Тогда массы примерно равны:
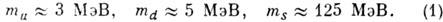
Если пренебречь массами кварков, то поля и-, d-, s- кварков не различаются и лагранжиан КХД инвариантен относительно вращений в пространстве типа (аромата) кварков (см. Внутренняя симметрия), при к-ром и-, d-,s-кварки переходят друг в друга. При этом вследствие векторного характера взаимодействия кварков с глюонами можно независимо вращать левые и правые составляющие кварковых полей qL , qR . Преобразования такого рода характеризуются 8 независимыми параметрами
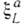 для левых частиц и 8 параметрами
для левых частиц и 8 параметрами 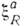 для правых (а=1, . . ., 8):
для правых (а=1, . . ., 8):
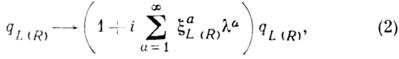
где
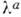 - Гелл-Мана матрицы, действующие в пространстве аромата кварков и, d, s.
- Гелл-Мана матрицы, действующие в пространстве аромата кварков и, d, s.
Если
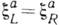 , то преобразования (2) сохраняют чётность. Инвариантность относительно таких преобразований имеет место и в том случае, когда массы кварков отличны от нуля, но равны между собой, т и = т d
, то преобразования (2) сохраняют чётность. Инвариантность относительно таких преобразований имеет место и в том случае, когда массы кварков отличны от нуля, но равны между собой, т и = т d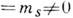 (исторически такая возможность обсуждалась первой). Как следует из (1), сейчас нет оснований полагать, что приближение равных масс кварков лучше приближения нулевых масс. В последнем случае лагранжиан инвариантен относительно преобразований и с
(исторически такая возможность обсуждалась первой). Как следует из (1), сейчас нет оснований полагать, что приближение равных масс кварков лучше приближения нулевых масс. В последнем случае лагранжиан инвариантен относительно преобразований и с  к-рые не сохраняют чётность (при преобразовании чётности, т. е. пространственной инверсии,
к-рые не сохраняют чётность (при преобразовании чётности, т. е. пространственной инверсии,  ) и наз. киральными преобразованиями.
) и наз. киральными преобразованиями.
С матем. точки зрения инвариантность относительно преобразований (2) означает киральную SU(3)
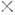 SU(3)- симметрию лагранжиана сильного взаимодействия. Если считать, что
SU(3)- симметрию лагранжиана сильного взаимодействия. Если считать, что 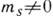 , но по-прежнему mu=md=0, то инвариантность лагранжиана сводится к группе К. с. SU(2)
, но по-прежнему mu=md=0, то инвариантность лагранжиана сводится к группе К. с. SU(2)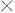 SU(2). Наконец, в приближении
SU(2). Наконец, в приближении 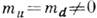 остаётся только SU(2 )-симметрия, к-рая отождествляется с изотопической инвариантностью сильного взаимодействия.
остаётся только SU(2 )-симметрия, к-рая отождествляется с изотопической инвариантностью сильного взаимодействия.
Исторически приближённая SU(3)
 SU(3 )-симметрия была открыта до того, как была сформулирована КХД. Феноменологически эта симметрия проявляется в существовании восьми относительно лёгких псевдоскалярных мезонов
SU(3 )-симметрия была открыта до того, как была сформулирована КХД. Феноменологически эта симметрия проявляется в существовании восьми относительно лёгких псевдоскалярных мезонов 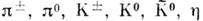 и в определённых соотношениях между амплитудами взаимодействия этих мезонов. Точной SU(3)
и в определённых соотношениях между амплитудами взаимодействия этих мезонов. Точной SU(3) SU(3 )-симметрии соответствует приближение нулевых масс кварков; в спектре адронов ей отвечает приближение
SU(3 )-симметрии соответствует приближение нулевых масс кварков; в спектре адронов ей отвечает приближение 
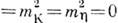 . Точная SU(2)
. Точная SU(2) SU(2 )-симметрия требует только
SU(2 )-симметрия требует только 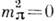 . Безмассовость мезонов отвечает при этом спонтанному нарушению К. с. (см. Спонтанное нарушение симметрии) - псевдоскалярные мезоны являются голдстоуновскими бозонами. Соотношения между амплитудами рассеяния этих мезонов можно получить, исходя из алгебры токов и используя частичное сохранение соответствующего аксиального тока (см. Аксиального тока частичное сохранение).
. Безмассовость мезонов отвечает при этом спонтанному нарушению К. с. (см. Спонтанное нарушение симметрии) - псевдоскалярные мезоны являются голдстоуновскими бозонами. Соотношения между амплитудами рассеяния этих мезонов можно получить, исходя из алгебры токов и используя частичное сохранение соответствующего аксиального тока (см. Аксиального тока частичное сохранение).
Лит.: Вайнштейн А. И., Захаров В. И., Частичное сохранение аксиального тока и процессы с "мягкими" p-мезонами, "УФН", 1970, т. 100, с. 225; Вайнштейн А. И. и др., Чармоний и квантовая хромодинамика, "УФН", 1977, т. 123,0. 217; Рамон П., Теория поля, пер. сангл., М., 1984.
В. И. Захаров.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
