- ИМПУЛЬСНОЕ ПРЕДСТАВЛЕНИЕ
- ИМПУЛЬСНОЕ ПРЕДСТАВЛЕНИЕ
-
квантовой механики ( р -представление) - описание квантовомеханич. систем, основанное на разложении векторов состояния|j(t)> по базисным векторам |p1, р2,. . .>, отвечающим определ. значениям импульсов р1, р2, . . . каждой из частиц. Если число частиц п фиксировано, то
где амплитуда < р1, р2, . . ., pn|j(t)> представляет собой n-частичную волновую ф-цию в И. п. Вероятность того, что в момент времени t импульс 1-й частицы лежит в интервале ( р1, p1+dp1), импульс 2-й частицы - в интервале ( р2, p2+dp2 )и т. д., пропорциональна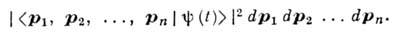
Если взаимодействие в системе зависит лишь от относит. расстояний между частицами и отсутствуют внеш. поля, нарушающие однородность пространства, то полный импульс P=p1+p2+...+pn сохраняется и его можно обратить в 0, переходя в систему центра масс частиц. В результате число независимых импульсов, от к-рых зависит волновая ф-ция, уменьшается на единицу. <Сопоставим И. п. с конфигурационным представлением, ограничиваясь для простоты случаем одной частицы. Пусть j( р)=< р|y> - волновая ф-ция данной частицы в И. п. По определению, оператор импульса
при этом диагоналей:
. Оператор координаты выглядит как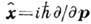 
, что согласуется с перестановочными соотношениями 
, dik - символ Кронекера. Переход к конфигурац. представлению, в к-ром волновая ф-ция частицы имеет вид j(x)=<x|y>, осуществляется с помощью трёхмерного преобразования Фурье:
Обратное преобразование отличается знаком в показателе экспоненты: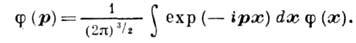
Симметрия между прямым и обратным преобразованиями Фурье является причиной сходства формулировок теории в импульсном и конфигурац. представлениях. В нек-рых случаях эти две формулировки оказываются тождественными. Так, операторы угл. момента
имеют один и тот же вид в обоих представлениях:
и т. п. Ещё один подобный пример даёт задача о линейном гармонич. осцилляторе с гамильтонианом
( т- масса осциллятора, w - частота). При её решении можно применять как И. п., так и конфигурац. представление. В обоих случаях волновая ф-ция будет выражаться через полиномы Эрмита (см. Ортогональные полиномы), что находится в соответствии с инвариантностью этих полиномов относительно преобразования Фурье. <Наиб. важное и адекватное применение И. п. находит в квантовомеханич. теории рассеяния, в частности в формализме Липмана-Швингера (см. Липмана-Швингера уравнение). Особенно возрастает роль И. п. при переходе к релятивистскому описанию взаимодействий частиц в квантовой теории поля, где оно объединяется с энергетич. представлением в рамках одного четырёхмерного р -представления. Конфигурац. представление здесь менее употребительно ввиду невозможности локализации релятивистских частиц с точностью лучшей, чем комптоновская длина волны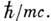
В. Г. Кадышевский.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
